In 2011, I
produced some review documents of a pending Hively and Horn article, submitted
for publication to Mid Continental
Journal of Archaeology, regarding
the Newark earthworks and what those authors call the “zero-degree hypothesis”.
This present document contains portions of those reviews that were transmitted
between myself, Hively and Horn, and the editor of Mid Continental Journal of Archaeology. These analyses are heavy on
GIS analysis.
The author grants
permission to reproduce text, tables, maps, or images included herein, provided
that the author is cited as Turner, Christopher S., year of article, name of article, conference
event and date (if applicable to the paper), page, and source, and provided
that use of any text, tables, maps, or images included herein is for
non-commercial, academic purposes only.
Review of
Some Research by Hively and Horn, with maps
Christopher S. Turner
2011
Here I will present a detailed
analysis of the primary sightline from authors’ backsight locus H1. As noted herein,
the viewshed of this sightline is obscured by local terrain with respect to the
Fairground Circle, but from H1 the Octagon group can be seen. It is this latter
sightline I will be examining.
I quote here in full the
authors’ premise concerning the methodology that forms the basis of the Hz
model (i.e. the “zero degree horizon model”):
“The HZ hypothesis makes a very specific
prediction about each linear Octagon feature that is aligned to a zero-altitude
standstill direction: if a line is
extended backward from the Octagon feature along the line of the standstill, it
will ultimately pass over a prominent elevation from which the zero-altitude
alignment could be conveniently observed.” (page 27 of manuscript, italics
authors’).
They continue:
“The valley in which the earthworks reside is surrounded
in all directions by the Appalachian foothills.
Consequently, the prediction that any line would pass over a commanding
overlook was likely to be satisfied by chance alone.” (page 28).
The chance of these loci randomly
occurring would be much less if the authors insisted on the extended sightlines
traversing a peak feature in the topography. If plotted using the authors’ data,
none of the four “H” points are on peaks. H2 and H4 are quite close however. H1
is on the incorrect side of a salient area, and H3 is on the incorrect side of
a ridge. (By incorrect, I mean that the authors’ proposed viewsheds are not
realized from these loci.) I suspect that the four “H” backsights would plot
nearer to or even upon peak features if the authors had used a finer grained
mapping system.
In any case, if these suggested
backsights are not at discrete geographic peaks, it can be argued that the
authors selected the sites to fulfill the demands of the model that they
function as dual backsights for lunar maxima and minima sightlines.
Preceding now with the analysis of
locus H1, if we follow the model as quoted above, we will extend the sightline
backward (i.e. to the southwest) from the axis of the octagon earthwork. As
noted by the authors in their 1982 paper, the azimuth of this line is 52.0ᵒ. This is based on a combination of methods: their own
field survey, the Middleton / Fowke data, and aerial photographs. I also
surveyed the axial azimuth in the field (in 1982), and obtained a figure of
52.1ᵒ. Using essentially the same methods as the authors, I
can concur that the figure they arrived at is acceptably accurate. Let the
azimuth figure then for the axis of the octagon and circle earthwork equal 52.0
degrees for this analysis.
It should be recalled that circa 1980,
the best maps available for these analyses were USGS topographic 7.5’
quadrangles. As I recall, a millimeter on these maps was equal to 78 feet (in
Chillicothe). I used to utilize a 1/64” ruler and a jeweler’s loupe to gain the
best accuracy possible in map analyses. Compared with the software that is
presently available, these methods now seem primitive.
In 1982, the authors’ calculations
were based on the first gleam event of the moonrise, whereby in computations
the factor for semi-diameter that represents this quantity (q) is set to (q =
-0.26 degree). As such, the authors found that the axial azimuth at the octagon
(A = 52.0ᵒ) yielded a resultant declination that was two-tenths
degrees in error.
It can be shown that if the authors
had used a value of (q = 0), [rise event for central bisection of the lunar
disc, i.e. the moon half risen], then the sightline would have been exactly
perfect for the event in question (i.e. the north lunar maximum rise for circa
1AD).
As such, I will present the remainder
of these analyses with the q-value set to zero (i.e. for central bisection of
the rising moon, that is, for the moon half-risen).
Following the authors’ premises, the
visible horizon as seen from the elevated backsight H1 has a lower apparent
angular height. It can be shown that the angular height along the sightline
with azimuth = 52.0ᵒ is in fact near zero degrees as the
authors suggest. This is a full half-degree lower than the same value as seen
from the Observatory Mound as posited in the authors’ 1982 paper for the same
sightline. This changes the resultant declination as viewed along the
sightline.
Using the q-value of zero, the resultant
declination as seen from H1 is +28.4, or four-tenths degree in error from the
lunar maximum. Even if the q-value is speciously “tweaked” to try to obtain a
“best fit”, the error is still present and is two-tenths degree.
The question then becomes, what
azimuth produces the correct sightline as seen from the authors’ H1 point? It
can be shown that the correct azimuth is 51.4ᵒ if the q-value
is left at zero.
In the diagrams that follow, it will
be noticed that the sightline if so plotted from H1 misses the axis of the
octagon entirely. At the location of the connecting neck between the octagon
and the circle, it misses by 78 meters. The lateral shift in the locus of the
horizon foresight is 162 meters.
These “errors” may be the results not
of an incorrect model, but on the low scale plotting of the locus of H1 by the
authors.
I will include this present document
and that from yesterday describing the use of the “q-value” in a complete
analysis of the H1 backsight.
My next step will be to re-analyze the
sightline from alternative locations of H1. My guess is that the incorrect
locus as provided by the authors is due to the low scale nature of their maps.
This plotting may also however reflect a desire on their part to have the
proposed sightline function as a “dual backsight” with regard to their proposed
Fairground Circle sightline. The more exactly these backsights can be plotted,
the more precisely a location can be suggested for archaeologists to investigate.
It would be preferable as regards hypothesis testing at these sites that their
locations be predicted in advance with the utmost care and precision.
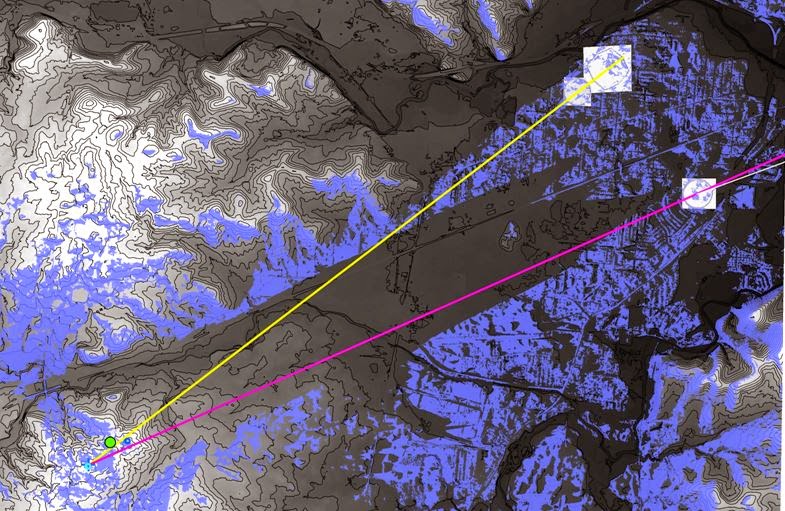
Figure 1. The yellow line from H1 lies along the azimuth of
52.0 degrees, and passes axially through the octagon and Observatory Circle
with reasonably good fit at this map scale. It should be remembered that this
value of 52.0 degrees was calculated using survey data collected circa 1885 and
by using paper maps, so some error should be expected at a finer scale when
plotted using ArcMap. This is especially so when the line is extended many
kilometers from its origin at the authors backsight H1.
Figure 2. Here is the environs of the landform which hosts
the authors’ proposed backsight H1. The distance from H1 to Point D is about
210 meters.
Figure 3. This is the horizon foresight locus for the
sightline with azimuth 52.0ᵒ
as seen from H1. It lies at a distance of 15428 meters from H1. The pink shaded
areas are visible from H1 according to the ArcMap viewshed analysis.
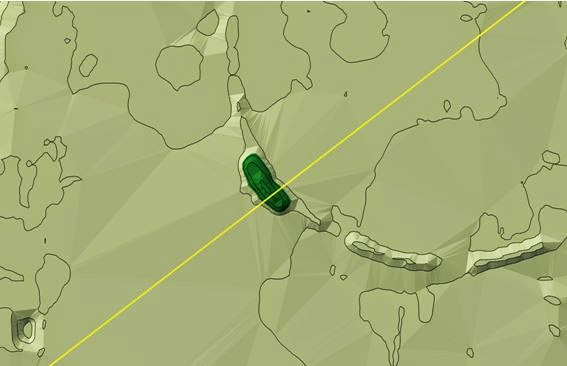
Figure 4. Here is the sightline where it passes near vertex
E of the octagon.
Figure 5. Here is the sightline where it passes through the
connecting neck at the same earthworks. This image is a combination of 1/10
meter elevation contours, the Middleton / Fowke plat for the octagon, the
Holmes map for the circle, and some plotted points from the Middleton / Fowke
survey (green dots).
Figure 6. The H1 sightline at the Observatory Mound.
Figure 7. A wide view of the same sightline: 1/10 meter
elevation contours. This line with azimuth of 52.0 degrees originates at authors’ backsight H1
some 7000 meters from the Observatory Mound. Over that distance, the skew of
the azimuth relative to the local axis of the octagon becomes apparent. The
azimuth of 52.0 degrees is functionally correct within the local confines of
the earthwork, but is relatively inaccurate over large distances.
Figure 8. The red line is the sightline with azimuth of 51.4ᵒ as seen from the authors’ H1
backsight locus. This sightline conforms to the north lunar maximum rise
declination as seen from H1 for the semi-diameter value (q = 0). If the q-value
were set to (q = +0.26ᵒ), i.e. for
the tangent rise event, then the sightline with the azimuth corresponding to a
declination for north lunar maximum rise would lie midway between the two lines
as shown and would still miss the connecting neck entirely (i.e. said line
would have an azimuth = 51.7ᵒ).
Figure 9. Detail view of Figure 8. Sightlines are 78 meters
apart at the location of the neck. The sightline plotted for a semi-diameter
value of (q = +0.26ᵒ) and a
resultant lunar rise azimuth of +28.8 degrees would still be offset from the
yellow line by 39 meters, missing the neck entirely.
Figure 10. Location of horizon foresights for sightlines
from H1: red line azimuth = 51.4ᵒ,
yellow line A = 52.0ᵒ. Corresponding declinations for (q = 0) are
+28.8ᵒ and +28.4ᵒ.
The goal of this phase of analysis was to obtain the most
accurate axial line with regard to the octagon and Observatory Mound
combination. The process was quite tedious. First, I had already converted all
of the Middleton / Fowke survey data points from “azimuth-distance” figures to
an X – Y grid. (I arbitrarily used vertex B as the (0,0) origin). The outline
of the octagon in ArcMap was created using these data points. They were merged
into the extant map layers as based on the UTM coordinates.
Middleton and Fowke had measured the width of the connecting
neck between the two polygons, and these reference points were the most crucial
in determining axiality at the enclosures. These four points are labeled 1, 34,
36, and 37 in their survey. They also measured the midpoint of the neck at the
circle, labeling this as point 0.
I had to create a
corresponding midpoint for the neck where it meets the octagon by measuring
halfway between points 36 and 37.
It was these two points, the one I created midway between
36-37, and the Middleton / Fowke point 0, that formed the central basis for my
analysis of the true axis of the earthwork group.
There was a great deal of trial and error as I shifted the
extreme ends of this line at its southwestern terminus near the original H1
locus, while alternating with nudging the northeast terminus of this axial line
at the horizon foresight area. After repeated iterations, I managed to get the
line within 0.01 meter of each point along the central axis of the connecting
neck at the earthworks.
Once this line was generated, it was checked relative to
other indices of axiality. For instance, the line misses the centroid of the
Observatory Circle by only 0.23 meters.
It is much more difficult to know with any certainty where
the exact center of the Observatory Mound is located. The line passes over the
highest contour lines in the ArcMap display, but reconstructions of this
earthwork make this index unreliable. I measured three other centrality indices
of this mound: the midpoint of the flat top of the mound, the midpoint of its
base, and the midpoint of the two fork features that extend out the mound to
the southwest. These three centers so measured are in close agreement, and a
point that approximates the three of them is 1.7 meters from the axis as
determined by the Middleton / Fowke points in the connecting neck.
Lastly, there is the location of the axial line as it passes
through the octagon vertex E. Again, it is quite difficult to gain an accurate
measurement of the embankment features with any certainty, but simple visual
inspection of the display in ArcMap shows a very good fit to the vertex.
Once the true axial line was determine in this manner, the
most likely backsight and foresight loci were plotted and measured. The
astronomical data were computed and the resultant lunar declination was
determined. The intervisibility of the points was checked using the ArcMap
viewshed function. Following are the explanatory graphics.
Figure 11. Detail of neck with Middleton / Fowke points 0,
1, 34, 36, 37, and the corresponding midway point between 36 and 37. The axial
line passes through the latter point and point 0 to within 0.01 meter of each
point, exceeding the accuracy of the survey data themselves. (Note: the Holmes
and Thomas plats were not used as regards point placement: they are for visual
orientation only.)
Figure 12. Detail view of vertex E and axial sightline with
scale bar.
Figure 13. Observatory Mound. As noted in the text, three
indices were measured to determine the center point of the mound’s long
dimension. The major axial line of the earthwork group (black) passes within
1.7 meters of a best fit line of these three measures. Contours are 1/10 meter.
Figure 15. Backsight area in USGS 7.5’ format with scale
bar. Note houses on peak with proposed backsight point. Green dot at elevation
of 341 meters.
These are the UTM data for the backsight and foresight of
the plotted axial sightline:
backsight (green dot in figures):
370414.58
4429722.384
foresight (yellow dot in figures):
383012.28
4439368.673
Elevation are 341 and 345 respectively (meters)
Corrected angular horizon height = (0 – 0.58 + 0.95) = +0.37
Azimuth = 51.47ᵒ
This results in a
declination of +28.8 for q = 0
(bisection of rising moon). This
is exactly correct for north lunar maximum rise circa 1AD.
It should be
noted that the Fairground Circle is shown as visible in the ArcMap viewshed
analysis from the proposed backsight (Figure 19).
My next step will
be to check the data on the Fairground Circle sightline as seen from the axial
sightline backsight (marked point C in Figures 2 and 31).
That should be
the last step to reanalyzing the H1 locus backsight.
It appears that
both the backsight and the foresight as defined by the axial sightline are at or on peak features, unlike Hively
and Horn’s proposed locations, which are on sloping areas This is likely due to
their use of low scale maps.
_________________________________________________________
Using the backsight point C as defined by the axis of the
Newark Octagon, here I analyze the sightline through the Fairground Circle as
seen from the same backsight. This backsight is 406 meters to the
south-southwest of the authors’ proposed H1 backsight. This backsight is 11
meters from a local topographic peak feature, and is at elevation 341 meters.
A line is created in ArcMap made to run from this backsight
so defined through the centroid of the Fairground Circle. The centroid of the
Fairground Circle is only 2.46 meters from the “center” of the Fairground
Circle as defined by the Eagle Mound and the sub-mound postmolds as mapped by
Greenman. This difference in the two loci is nominal.
The sightline is extended in ArcMap to the northeast through
the Fairground Circle centroid till it encounters elevated landforms that
create the visible horizon as seen from the backsight locus. Using the viewshed
analysis feature in ArcMap, the foresight is defined along the sightline that
is visible from the backsight.
The horizon foresight so defined lies at 20930 meters from
the backsight locus point C. It actually has an elevation that is lower than
the backsight! I checked for other
foresight loci out to a distance of 38 kilometers none were found. There are
likely very small sections of more distant horizon that merge together forming
the visible horizon as seen from the backsight locus. These would be
impractically distant from the backsight for prehistoric use, and the effective
angular horizon height of these distant foresights would not differ from the
one selected at 20930 meters. All of these areas effectively present a “zero
degree horizon” as seen from the backsight locus.
The positional data of the proposed foresight were obtained
using ArcMap, and these data were analyzed for astronomical significance.
The following graphics illustrate the results.
Figure 25. Google Earth image of foresight loci. Note how
both possible foresight loci are still in tree cover. They may have greater
archaeological integrity than many of the other potential foresight loci in the
Newark area.
Figure 29. General view of sightlines as seen from point C:
axial octagon line, Fairground Circle line from same backsight.
The azimuth of the line from the axial octagon backsight
through the centroid of the Fairground Circle is A = 64.81 degrees.
The effective angular horizon height along this line is that
of a “zero degree horizon”. As such, the corrected horizon height hc = 0.37 degrees.
The resultant declination along this sightline is = +19.3
degrees for a q-value = 0 (bisected rising moon).
This is in error from the declination of the north lunar
minimum rise by 7/10 degree, or 1.4 moon widths.
This is an appreciable error and should not be discounted,
especially in that the sightline through the octagon axis is exactly correct
for the north lunar maximum rise event.
The authors at various points in their manuscript suggest
that errors of 0.5 degrees are insignificant. Degrees of precision with such
great error ranges are unacceptable. With a higher precision treatment of the
data, use of a mapping system that can afford such precision, and by rigorously
maintaining a fixed use of a particular q-value (preferably q = 0), the
precision of resultant data becomes possible.
The Newark Octagon and the Fairground Circle are the two
best preserved Hopewell geometric enclosures, and afford the best chance at
determining high precision sightlines. By using remote sensing as has been
employed at the Hopeton site in Chillicothe, similar degrees of ground accuracy
can be obtained. The recent availability of USGS 1/9” DEMs further augments the
ability to produce precision analyses of sightlines, vitiating any validity of
claims that we need be satisfied with declination values of wide ranging uncertainty.
The authors are imprecise as regards their use of error
range and just what constitutes an error. It is difficult to follow whether
they are referring to an error in the resultant declination value when
referring to a sightline, or in the error of the specific azimuth of the
sightline. The two are not mutually interchangeable.
For instance, in the calculations for the Fairground Circle
centroid sightline, the azimuth value used is 64.8 degrees. Consider the same
equation for the two azimuth values 64 and 65 degrees. The corresponding
declinations are +19.9 and + 19.1, a difference of 8/10 degree resulting from a
one degree change in azimuth. This 2/10 degree difference may seem like a
trivial amount until it is remembered that the target object in question, the
moon, is itself only 0.5 degree in diameter.
More rigorous control of error tolerances must be
demonstrated and maintained.
At one point in their manuscript, specifically referring to
the locus of backsight H1, the authors suggest that a change in the ground
locus of this backsight of 60 meters is acceptable! They suggest that this
would alter the resultant azimuth value by up to 0.5 degrees, and they suggest
that this is acceptable!
Many of the error tolerances cited by the authors as regards
their 1982 paper are due to systematic errors. The authors employ a spurious
non-parsimonious method of defining what constitutes a sightline. Part of their
argument uses the spine or ridge of given octagon embankments to define
astronomically significant azimuths. But, in other sections of their 1982 and
1984 (and in the present) papers, they define these astronomically significant
sightlines as being defined by the edges
of the vertex gateways or gaps. These “gap edge” sightlines form a major
thrust of the authors’ argument of “deliberate distortion” of the otherwise
geometrically regular octagon (see page 14 manuscript and the 1982 article),
and are not trivial in importance or frequency.
It can be shown that the sightlines that the authors have
chosen to define as existing along the spines or ridges of the embankments can
also be as accurately defined by the vertex gateway or gap features, and their
corresponding edges.
It is these sort of sightlines that the authors’ themselves
define in key examples at the Newark octagon (1982), and at the great majority
of their sightlines at the High Bank earthworks in Chillicothe (1984). The
authors are in essence choosing again which set of data fit which desired
computational outcome, as has been demonstrated to be the case with their
varying use of the q-value factor.
As with the q-value factor, the most parsimonious procedure
would be to adhere to one and only one framework within the model. Because the
embankment ridgeline azimuths can be as effectively generated with the
gap-to-gap interpretation by the same data, but not vice versa, it follows that
the authors should abandon the ridgeline or embankment spine model and adhere
to the gap-to-gap interpretation. From a scientific and experimental viewpoint,
it cannot be had both ways.
This issue is not without importance as pertaining to the
citing of error ranges and values. Because the authors claim to maintain an
adherence to the ridgeline azimuth model, they are forced to cite high error
ranges of 1.7 degrees in their 1982 paper. (Actually the error they cite in
1982 is 1.3 degrees, but it is cited elsewhere as 1.7 degrees).
It is this error value which compels them to commend the new
Hz or “zero degree horizon” model. Now, after reviewing their premises, I am
convinced, with some corrections, that they have discovered a valid model that
was used by the Hopewell in designing and constructing the Newark Octagon. The
issue here I am addressing is rather that of error tolerances, not the Hz model
itself.
The authors state in their manuscript that the Hz model
still produces errors of 1.6 degrees, or a 1/10 degree difference from the
model on which they were trying to improve! Note here how it is difficult to
determine if they are referring to azimuth values or declinations values, as
they do not rigorously define these.
In effect, by citing a resultant error range of 1.6 degrees
for a model that they consider to be valid, they are asserting that such a
great error is acceptable in the analysis of astronomically significant
sightlines. It is this point I would contest specifically. An error of 1.6 degrees is over three moon
widths. Also recall that the authors do not rigorously treat the use of the
q-value, which can introduce a further 4/10 degree range in citable resultant
declination values.
Elsewhere in the manuscript, the authors suggest that the
combination of the Middleton / Fowke survey data when assessed with their
topographical analysis should produce an accuracy of 0.1 degree in azimuth
values. (page 28 of manuscript)
Inasmuch as the authors suggest a precision value of 0.1
degree, it seems to be entirely implausible on the other hand to accept as
valid astronomical sightlines that result in error values as high as 1.6
degrees.
In my own present analysis of the lunar minimum sightline as
defined through the center of the Fairground Circle centroid as viewed from the
locus of the octagon’s axial backsight, point C, the declination error along
this sightline is 7/10 degree, or 1.4 moon widths. To me this seems
unacceptably large itself to be cited as anything approaching validity within
the model. This is especially true when we consider the high degree of
precision (essentially perfect) in the axial sightline of the octagon as I have
demonstrated regarding its indexing of the lunar maximum rise.
In their present paper, the authors cite errors of similar
magnitude in their analysis, and claim them as valid astronomical sightlines,
or “alignments” as they call them.
The authors seem to want to have it both ways. They assert
claims of precision of 1-meter for the Middleton / Fowke survey data. They cite
topographic azimuth accuracy of 1/10 degree. But when their proposed sightline
declinations are off by 0.5 to 0.9 degree or more, they brush such errors aside
as being due to imprecision in the method of analysis or to the imprecision of
the observations made by the Hopewell.
To make such
suggestions is to ignore the means by which we can improve the handling of
these data, and anthropologically it smacks of an ethnocentric assessment of
the observational acuity that was manifested and employed by the ancients. Actually, many of the authors’ proposed
errors can be shown to be a result of poor modeling, insufficient map accuracy
tolerances, misuse of the q-value, or a combination thereof.
As an important side bar: I completely reject the authors’
claim that the azimuth of the rising point of the moon can vary laterally due
to refraction by as much one degree (see page 12 manuscript), or even by a
total of +/- one degree depending on how one reads this sentence. I have been
observing the sky for 40 years and I have never experienced such a wild range
of refraction effects. Such an effect would be plainly visible while observing
the rising of a bright star.
The authors have suggested the Hz model by the following
premise: we take the extant sightlines at the octagon and reverse the azimuths
till we arrive at salient features in the topography. I have done just that, as
accurately as possible assessing the axial value for azimuth of the Newark
Octagon group. This line does not eventuate in the locus of H1 as defined by
the authors. It rather culminates within 11 meters of a peak feature, and the
resultant declination from that peak area as pertains to the north lunar
maximum rise event is exact.
Furthering with the author’s model, when the sightline for
the Fairground Circle centroid is tested from this same backsight, it fails to
demonstrate astronomical significance. It misses the declination in question by
1.4 moon widths, an unacceptably large error given the treatment of the data.
The authors assert that the selected backsight locus of H1
is unto itself topographically salient and that they have not chosen this locus
speciously with regard to satisfying the criteria of their model. However, the
location of H1 is in fact on the slope of a ridge feature, at a non-salient
location. The Fairground Circle is not even visible from H1. There is no logical
reason to choose H1 as the backsight locus as opposed to others that may lie
along this particular azimuth.
When tested using ArcMap, the authors’ proposed sightline
from their H1 backsight to the Fairground Circle is obscured by local terrain.
The azimuth between H1 and the Fairground Circle does approximate the location
of the north lunar minimum rise however. As such, it appears as if the authors
have chosen this placement for this proposed backsight H1 more with regard to
meeting the needs of their model than as to having objectively followed their
own criterion as defined for placing these elevated backsights. Of all of the
possible locations along their proposed sightline that they may have placed
this backsight, they chose the one that “worked” with regard to the Fairground
Circle.
Having said this, I would like to state that I still believe
that the authors have discovered a valid geographic set of (approximate)
locations that were used by the Hopewell in designing and constructing the
Newark Octagon. I believe that it can be shown that peak features were the
preferred loci of these backsights. I think that the errors with regard to the
authors’ proposed locations of these elevated backsights are due to their use
of low scale mapping and can and should
be improved.
More GIS review of H1 properties
I begin with the authors’ value of H1 as noted in the
article, i.e. latitude = +40.0123, and longitude = -82.5150. (page 29 of
manuscript)
H1 is the authors’ locus = lat +40.0123, long -82.5150 as
provided by authors on page 29 of their manuscript. These values were converted
to UTM zone 17 coordinates 4430012 and 370697 for the NAD 1927 datum, using the website http://www.rcn.montana.edu/resources/tools/coordinates.aspx
, then the location was determined and plotted using ArcMap 9.3
Points C and D are considered below as alternative loci for the
authors’ proposed backsight.
Figure 32. This is the line plotted from authors’ H1
backsight to vertex “E” of the octagon
Figure 33. This is the line (purple) from H1 through the
Fairground Circle center. The white line is the approximated axial sightline
for the Fairground Circle.
Notice how the authors’ suggested
sightline (purple) is skewed relative to the axis of the center and gateway of
the Fairground Circle. The authors argue that the enclosure is an imperfect
circle and as such does not have a true “center”, so that there is room for
variance in this regard. While the enclosure is not as geometrically regular as
the circle at the nearby octagon, it has a distinguishing feature unlike most
such Hopewell enclosures. I refer to the central mounds. These four low mounds
are known collectively as the “Eagle Mound”. Greenman excavated this mound
group around 1930, and uncovered as series of post molds that are consistent
with a rectangular structure whose long dimension is collinear with the axis
defined by the gateway.
One has to ask
certain questions regarding the authors’ interpretation of the sightline shown
above in purple. They note that from the point H1, the two lines, one to the
octagon and one to the Fairground Circle, define the north lunar maximum and
the north lunar minimum rise points respectively.
As for the line to
the Fairground Circle, it has only an imperfect fit. One has to ask, given the
exactitude and construction ability demonstrated by the line to the octagon:
“Why isn’t the line to the Fairground Circle more accurate?” It can be defined
as crossing the Eagle Mound in the center, or as passing centrally through the
gateway, but not both. Why would the
builders not place the Fairground Circle’s gateway in a more accurate location?
Also, and this is
very important, there are issues of landscape phenomenology that need to be
addressed. These methods of investigation, developed by British archaeologists,
are largely ignored within Hopewell archaeoastronomy.
At this point in
time, the best evidence suggests that the construction of the Fairground Circle
preceded that of the octagon. Brad
Lepper and other archaeologists excavated a section of the wall at Fairground,
and obtained datable material which suggests a construction date early in the
Middle Woodland period, around 100BC. Lepper was also involved in obtaining
datable material from the octagon site, and these dates are much later, around
AD 300. Even given vagaries in dating,
these dates suggest that the construction of the Fairground Circle preceded the
construction of the octagon.
The Fairground
Circle also has been suggested by several researchers: Carskadden and Morton,
myself, and later Byers, to in essence be a Late Adena circle. This is based on
its morphology. The great majority of Hopewell enclosures do not have interior
ditches, but Fairground notably does. Its singular opening to the northeast is
also an Adena trait. One could even suggest that its geometric irregularity may
be indicative of an early placement in the chronology of Hopewell enclosure
construction. The exactitude found at the octagon can argue for its later
construction.
Now, to return to
landscape and phenomenology, and to châine
opératoire reasoning. When humans observe the sky, it must be
that first sedentism is occurring for horizon calendars to develop. This is
nearly an axiom in archaeoastronomy. Mobile groups use the zenith passage or
heliacal rising of stars to mark the seasons, whereas sedentary groups use the
sun’s motion along the horizon. The reason is obvious: if you are mobile you
will not grow accustomed to the location of celestial objects as they rise and
set along a specific local horizon.
There is also a
lineage defined by the dictates of the sky itself regarding the order in which
events become known to observers. Humans recognize the solstices before
anything else within the corpus of solar and lunar motions. There are citable
papers on this topic. In this regard, it is accepted that human observers would
need first a deep familiarity with the solar motions before they would ever
notice the more subtle variations of the lunar rise locations. This is why it
is fairly common to find evidence for solstice observations across the world,
whereas the lunar indices that the authors discovered at Newark are much rarer.
The least salient
of all of these lunar horizon loci are those of the lunar minimum events.
Whereas the lunar maximum rise and set points exceed the locations of the sun along the horizon, the lunar
minimum points are within the range
along the horizon of the sun’s movements, and indeed they are contained within the range of the moon’s azimuthal range along
the horizon. As such, they would be the most difficult to observe and index
definitively.
Hence, the notion
that indices to the lunar minimum would precede those to the lunar maximum is
fallacious. Yet that is what must be suggested in declaring the H1 sightline to
the Fairground Circle to be a lunar minimum line. If the dating and apparent
cultural chronologies regarding the Fairground Circle and the octagon are
correct, it is very unlikely that the authors’ interpretation can be valid. The
idea that the sightline to the Fairground Circle from point H1 was delineated intentionally
with regard to the lunar minimum rise point must be reexamined.
Figure 37. Areas in blue are the viewshed from Point C. The
Fairground Circle is visible from this point, but a large swath of the valley
remains obscured. Note variations in viewshed coverage as compared with Figure
19, which uses a lower scale DEM in analysis.
Figure 39. Detail of Fairground Circle: rose colored areas
are visible from Point D.
Code: green = visible, red = invisible from Point D
|
Figure 42. Sightline from
point D
Figure
46. An idealized axial sightline through the Fairground Circle is shown in
purple. Note where the “best fit” Fairground Circle sightline (Figure 45)
(purple) crosses the Octagon sightline (yellow). This would approximate the
“best fit” area for the authors’ proposed multiple backsight point when
considered for enclosure axiality of sightlines. The distance from Point D to
the crossing point of the two lines is 1430 meters, from authors’ H1 locus the
distance is 1620 meters.
The
three analyzed backsight points are shown at bottom of figure: H1 (green dot),
Point C (turquoise circle), and Point D (blue circle).
Calculations testing
authors’ proposed sightline to Fairground Circle from H1
Authors
give location of their point H1 as :
+40.0123 latitude, -82,5150 longitude
These
convert to (UTM Zone 17) = 4430012 northing 370697 easting
After
conversion to the form degrees-minutes-seconds, these figures can be entered
into the online azimuth calculator found at
giving
an azimuth value of 65.91ᵒ between authors’ H1 and the center of the Fairground
Circle.
I
checked the horizon features using ArcMap. The horizon as seen from H1 along
this azimuth lies 21.8 km distant. I
checked as far away as 37 km finding no other likely horizon loci.
The
elevation of H1 is near 332m , whereas the horizon terminus of the sightline
has an elevation of 315m. The difference is negligible at this distance, and
hence the horizon is effectively a “zero degree horizon” along this sightline
as the authors suggest.
For
calculation purposes, these are the positional data for the horizon locus:
Horizon foresight of
Fairground Circle (center) sightline as seen from authors’ backsight H1
UTM (Zone 17 NAD 1927) decimal
degrees degree,
minutes, seconds
391051 +40.09310 40 05 35.2 N
4438663 -82.27804 82 16 40.9 W
Using
the standard equation to obtain declination, the results are:
sin
δ = (sin φ)(sin h) + (cos A)(cos δ)(cos h)
φ
= latitude
A
= azimuth
h
= corrected horizon height
i.e. h
= (h₀ - r + p ) +/- q
where h₀
= true horizon height
r
= corresponding refraction value for that height [for h₀ = 0ᵒ , r = (-0.58ᵒ)]
p
= parallax value (for moon p = 0.95ᵒ, negligible for sun = 0.002ᵒ)
q
= +0.26ᵒ if for tangent event
q
= -0.26ᵒ for gleam event
q
= 0ᵒ for bisection of disk of sun or moon
Results show that for q = 0, δ = +18ᵒ.5
The declination value for the north lunar minimum
event circa 1AD was +18.6ᵒ, hence this line is within accuracy guidelines.
Remember though, the sightline is
actually obscured by terrain, and the circle is invisible from H1.
Testing the Sightline from Point D through
the Fairground Circle Center
If the same calculations are made for the
sightline from Point D to the center of the Fairground Circle as outlined in
the graphics above, the resultant declination δ = +18.8ᵒ.
This value is also within accuracy guidelines. If
the Hopewell skywatchers were observing the first gleam event, this value is
exact (i.e. for q = -0.26ᵒ, δ = +18.6ᵒ).
The geographic data for sightline D are as
follows:
Point D
(locus proximate to H1 with best view of valley)
UTM (Zone 17 NAD 1927) decimal
degrees degree,
minutes, seconds
370905 +40.0125 40 00
45.0 N
4430030 -82.512583 82 30
45.3 W
Horizon foresight
of Fairground Circle(center) sightline as seen from point D
UTM (Zone 17 NAD 1927) decimal
degrees degree,
minutes, seconds
390270 +40.09110 40 05
28.0 N
4438452 -82.28716 82 17
13.8 W
Distance of sightline to horizon is 21.12km
elevation of D is 335 m
elevation of horizon locus is 325 m
again indicating a “zero degree horizon” effect as authors
premise
Testing the
Octagon Sightlines from H1 and D
H1 (authors suggested backsight for octagon axis
and Fairground Circle center)
UTM (Zone 17 NAD 1927) decimal
degrees degrees,
minutes, seconds
4430012 (+/- 5.5m) +40ᵒ.01230 40ᵒ 00’
44”.3 N
370697 (+/- 4.5m) -82.5150 82 30
54.0 W
elevation = 332
Point D
(salient peak locus proximate to H1 with
best view of valley)
UTM (Zone 17 NAD 1927) decimal
degrees degree,
minutes, seconds
4430030 +40.0125 40 00
45.0 N
370905 -82.512583 82 30
45.3 W
elevation = 336
Horizon
Foresight from authors’ H1:
UTM
(Zone 17 NAD 1927) decimal degrees degree, minutes, seconds
4439292 +40.09579 40 05
44.849 N
383017 -82.37237 82 22
20.525 W
Continuing Review
of Author’s Article: (from page 27
through 30)
We then noticed that all the errors in the Octagon
alignments were small and of comparable value if we assumed that the Octagon
features were built along zero-altitude lines directed toward the lunar
standstills as would be seen from high elevations where the altitudes of
distant horizons were negligible. The HZ
hypothesis makes a very specific prediction about each linear Octagon feature
that is aligned to a zero-altitude standstill direction: if a line is extended backward from the Octagon feature along the line
of the standstill, it will ultimately pass over a prominent elevation from
which the zero-altitude alignment could be conveniently observed. At first we were skeptical about the
likelihood of finding persuasive evidence for this idea. The valley in which the earthworks reside is
surrounded in all directions by the Appalachian foothills. Consequently, the prediction that any line
would pass over a commanding overlook was likely to be satisfied by chance
alone. Accordingly we did not initially
think the possibility was even worth investigating because intentionality could
never be demonstrated. We were taken by
surprise to discover that the elevated overlooks predicted by HZ for
specific alignments in the earthworks were not only present in a prominent
fashion, but that they had a repetitive pattern of geometrical relations to the
earthworks and to one another which were unlikely to be due to chance.
Please propose the
method of statistical analysis here regarding the prior phrase “…were
unlikely to be due to chance”. It is difficult to imagine the statistical
format that would be used to analyze these varied multiple locations, though it
must be possible.
.
In the analysis that follows the azimuths between
earthwork features and positions in the local terrain have been determined
using USGS 7.5 minute quads and digital mapping programs (Delorme 2002, 2004).
The coordinates of earthwork features have been entered into the program using:
(1) on-site GPS measurements; (2) rectified aerial photographs of the
Earthworks; (3) the survey data obtained by James Middleton. Field checks (using GPS measurements) of the
azimuths obtained from the computer software suggest that unless otherwise stated
the likely errors in the azimuths between earthwork features and distant
locations in the local topography are on the order of ± 0°.1.
The first and most important test of HZ is
for the all-important alignment of the Circle-Octagon avenue axis to the
northern maximum extreme moonrise. When
a line is extended through the center of the Observatory Circle backward along
the avenue alignment at an azimuth 232°.0, we find that
the line passes very near the highest point on a plateau that provides the most
commanding overlook of the earthworks from the southwest. The highest point on this azimuth which
provides the best view of the valley below (known hereafter as point H1 and
shown in Figure 8) is located at latitude 40°.0123 N and
longitude 82°.5150 W. The
topographical profile from the Octagon center to H1 is shown in Figure 9.[i]
This is shown by above
graphics to be largely correct. The
octagon is visible from the authors point H1, but the Fairground Circle is
not.
The existence of H1 would not add much to the case for
astronomy at Newark if it were not related to another major feature of the
earthworks in a manner that is similar and complementary to its relation to the
Circle and Octagon. In our original
paper we noted that the Great Circle had an avenue opening with avenue walls directed (66°.68 and 66°.41
according to the Middleton survey recorded in Thomas, 462) toward the northern
minimum extreme moonrise (within 0°.5). The walls of
the avenue are far too short (25.6 m and 29 m) and asymmetrical, however, to
define an alignment to the horizon with an accuracy better than ± 1°.0. The center of the imperfect Great Circle and the center of the avenue
with asymmetrical walls cannot be unambiguously located, and so a line
between these two points does not produce a precisely defined alignment. Any alignment proposed for the center of the
Great Circle to the center of the outgoing avenue would be uncertain by 1°. The
best estimate available for that alignment would be about 69°.
So, the best that one can say
from the survey data internal to the Great Circle is that its avenue points in
the general direction of the northern minimum extreme moonrise (within three
degrees).
This paragraph is quite
problematic. First, the authors do correctly recount their assertion from
HH1982 that claims that the entry walls at the Fairground Circle define a lunar
minimum sightline. Yes, that is their claim in 1982. But as they acknowledge
above, these walls are exceedingly short,
bulky, and non-linear so as to be suggested as sighting devices. To do so
sets a bad precedent in this line of research, and neither they or has anyone
else followed up with such assertions.
Their statement above
that it is impossible to accurately define the center of the circle is quite
misleading. True, the large circle is irregular, and as such it is problematic
to define an unambiguous center. But, and the authors are well aware of this,
there is a small set of mounds near the middle of the enclosure called the
“Eagle Mound”. It can be shown in ArcMap that the geometric centroid of the
circle and the axial midpoint of the Eagle Mound are separated by less than
three meters (2.46 m).
Greenman circa 1930
excavated these mounds and found postmolds beneath them consistent with a long
rectangular structure having once existed there. The long axis of this
structure is coincident with the axis toward the gateway of the Fairground
Circle. Culturally speaking, it is evident that the Hopewell used this locus as
the “working” center of the Fairground Circle. As such, it is quite easy to
define the azimuth from the “center” of the circle to the gateway. The authors
above say it is about 69 degrees, which is reasonably near to what I have
surveyed in situ to be 68.5ᵒ
or 68.6ᵒ. These values can be determined mathematically from the
Middleton data or graphically from the Holmes map also, and agree.
It is beyond reasonable
to suggest that this sightline so established defines the lunar minimum rise
point, as Romain has claimed elsewhere. As the authors admit, it is 3 degrees
in error from this sightline. This error amount is far too large to suggest
anything conclusive. Three degrees is six moon widths!
The authors are
ignoring work that I have performed since 1982 related to this site. I have
shown in several papers and many conference presentations that the axial
sightline at the Fairground Circle defines the May cross quarter date, this
being around May 5. I interpret this as being a solar sightline used in
establishing a planting calendar. The Hopewell were beginning to depend heavily
on the cultivars of the Eastern Agricultural Complex, as can be shown in the
archaeological record, and it is a culturally plausible interpretation that
this circle was designed by elite skywatchers who were engaged in subsistence
scheduling.
It also brings to bear
a key point. No one would suggest that a human observer would begin monitoring
moonrises until well after they had become aware of solar sightlines. We can
employ the phenomenological premises of operational sequence studies to define
in what manner given celestial events would become recognized by human observers.
It invariably follows that solar motions are far easier to observe and detect
than lunar ones. The more subtle lunar motions would have to be preceded by
many generations of observers who were marking the solar motions. There are
several good journal and book articles in the archaeoastronomy corpus that
develop this idea. I am surprised that the authors do not use these as
guidelines, but are trying instead to suggest the preeminence of the lunar
sightlines exclusively, without providing any cultural background regarding the
development of this technology.
The significant observation to be made in this context,
however, is that if a line is drawn from H1 to the centroid of the Great Circle or
the ‘center’ of the outgoing avenue from this circle, the resulting azimuth
is 65°.9 (within 0°.2 of the
northern minimum extreme moonrise for zero altitude). Since H1 is located some 7.7 km from the
Great Circle centroid, uncertainties in
the positions of the centroid and the center of the outgoing avenue have a
negligible effect on the azimuth of this alignment. This alignment is shown in Figure 8, and the
topographical profile from the Great Circle centroid to H1 is shown in Fig
9.
I obtain the exact same
azimuth value for the sightline from the authors’ H1 point through the center
of the Fairground Circle, A = 65ᵒ.91. Recall however that this sightline is obscured
by nearby foreground terrain so that the Fairground Circle is invisible from
the authors’ H1 backsight.
The modeled sightline
is indeed within only 1/10 degree off the lunar minimum rise point, taking the
moon as “centrally bisected” at rising (i.e. q=0).
Notice the use of the
word “or” in this sentence, tacitly acknowledging that a line cannot be drawn
through both the center of the circle
and the center of the gateway at the
Fairground Circle that originates at the authors’ backsight H1: “…if a line is drawn from H1 to the centroid
of the Great Circle or the ‘center’ of the outgoing avenue from this
circle”…
This sentence is less
than clear: “..uncertainties in the
positions of the centroid and the center of the outgoing avenue have a
negligible effect on the azimuth of this alignment.”, As can be seen in the
graphics provided above, in no case do the avenue and the center of the
Fairground Circle fall along the same line as seen from the authors’ point H1.
Also, the use of the term “centroid” is superfluous, the de facto “center” of this circle would have been the locus of the
present Eagle Mound, and more specifically, the structure that once stood
there. The two points are only 2.46 meters apart.
Thus H1 (the most commanding overlook point to the
southwest of the earthworks) (is not, but rather on slope on west side of
ridge) provides a common backsight for the observation of two complementary
lunar standstills. From H1 an observer
would see the Moon rise over the Observatory Circle-Octagon axis when it was at
the northern maximum standstill. The same H1 observer would also see the
Moon rise over a line through the center of the Great Circle and its associated
avenue when the Moon was at the minor standstill. So as the Moon oscillated
back and forth between the major and minor standstills, it would (at its
northern extreme rise point) move back and forth between the center of the
Observatory Circle-Octagon and the centroid/avenue of the Great Circle as seen
from H1. The effects of the altitude of
distant horizons on these alignments is negligible (< 0°.05) and both
alignments as seen from H1 have an accuracy of 0°.3 or less. The location which might have been used for such
backsight observations cannot be determined exactly from these considerations
since the backsight (over 7.2 km from either circle center) could be moved by as much as 60 m without
producing alignment errors greater than 0°.5. On the other hand the position of H1 cannot
be moved further than about 50 m toward the southwest without losing a direct
view of the Great Circle.
Notice in the above
paragraph that the authors are very careful to state that the sightline to the
Fairground Circle passes “through the
center” of the circle, whereas the sightline to the octagon is genuinely
axial. This is a tacit admission that the proposed lunar minimum sightline
does not pass through the center of the
gateway of the Fairground Circle. Again, given the degree of accuracy found
with the axial alignment at the octagon, this begs the question why the
sightline (i.e. the gateway location) was not so constructed at the Fairground
Circle.
The authors suggest
above that the backsight locus H1 “could
be moved by as much as 60 m without producing alignment errors greater than 0ᵒ.5.”
This value of 0ᵒ.5 is quite high,
and would cause the moon to rise out of line by its entire diameter. The
sentence is therefore superfluous and should be deleted.
The authors also write:
“On the other hand the position of H1
cannot be moved further than about 50 m toward the southwest without losing a
direct view of the Great Circle.” As demonstrated in the above graphics,
the Fairground Circle is not visible at all from their proposed backsight H1,
and to remain as a plausible argument, the proffered locus needs to be
relocated to point C or D as outlined in the descriptions appended to the above
graphics.
No comments:
Post a Comment