High Precision Sightlines at the Liberty Earthworks

The Production and Analysis of High-Precision Calendrical Sightlines at 

the Liberty Earthworks,

Ross County, Ohio

The author grants permission to reproduce text, tables, maps, or images included herein, provided that the author is cited as Turner, Christopher S.,  year of article, name of article, conference event and date if applicable to paper, page, and source, and provided that use of any text, tables, maps, or images included herein is for non-commercial, academic purposes only.


I WILL INSERT THE REMAINDER OF THE FIGURES IN THE VERY NEAR FUTURE. CT May 2015











Christopher S. Turner
Carbondale, Illinois
2015



Abstract

Using Arc Map GIS software and an Excel spreadsheet programmed to process archaeoastronomical data, a Middle Woodland Ohio Hopewell geometric enclosure, the Liberty earthworks square, was analyzed to determine if calendrical sightlines were incorporated into its design. The results indicated multiple equinox and cross-quarter date indices, the latter similar to those found at the Fairground Circle and Hopeton earthworks. Some of the lunar extrema (or standstill) phenomena are also marked. Topographic maps of the horizon foresight loci suggested by the calendrical sightlines are presented. Arc Map software allows for an exact defining of proposed sightlines at a precision exceeding the error values of the input data, allowing for full utilization of those data. The presence of the May cross-quarter sightline corroborates those same sightlines found at the Fairground Circle and Hopeton sites. This “May Day” index suggests an incipient agriculture and associated subsistence scheduling, while the monumentality of the earthworks themselves, and the cognitive etiology embodied across the corpus of calendrical indices, evidences an enduring body of scheduling elites who developed and utilized the sightlines.





Preliminaries
The Liberty earthworks (33Ro22) is classic amongst the Hopewell geometric enclosures (Squier and Davis 1848:56-57). Located southeast of Chillicothe in Ross County, Ohio, the site though long degraded by European American farmers and pothunters has yielded substantial archaeological information (Greber 1979, 1983, Mills 1907). Similar to the Seip earthworks (33Ro40) and the Hopewell type-site (33Ro22), this set of geometrical figures was associated with a large loaf-shaped mound and other mortuary tumuli.
The monumental complex has been termed a "tripartite" enclosure (Figure 1). Like several other such Hopewell earthworks, Liberty featured two circles conjoined to a square. Analysis of the square enclosure is presented in this paper.
Survey data of the Liberty square from Thomas (1894:482) formed the basis of the analysis. Circa 1885, the Bureau of Ethnology in Washington DC sent the surveying team of James D. Middleton and Gerard Fowke to examine the Ohio geometrical sites, this in an effort to test the veracity of claims regarding their putative geometrical accuracy. Fowke (1889) noted “Nearly all of the enclosures of Ohio ...have lately been very carefully surveyed, and not a single “exact square” or “perfect circle” has been found amongst them, though some of the works approach very closely to these forms. There is sufficient accuracy in some cases to make one wonder that the builders could have done as well as they did…”. In another article (1902:171), Fowke commented on their survey, stating that “the angles, when not on the wall, are at the intersection of adjacent straight lines. All stakes were set as near the middle [of an embankment] as was possible by measure and judgment. Greater care was taken in getting bearings and distances than is usually employed in rail way or canal surveys. Middleton and I, who did the work, stand by our figures, and with all the more reason, too, that in some cases they completely upset our antecedent ideas and opinions.”
Middleton and Fowke in the 1880s were able to survey earthworks that held greater morphological integrity than those which we have today, closer in form to what was extant 1700-odd years ago. While at the Liberty earthworks, Middleton and Fowke noted that the small circle was still well defined, nearer in shape to the prehistoric original. “The smaller circle, however, is all in woodland or pasture, and could be surveyed without difficulty…[and]…especial care was taken in its measurements (Fowke 1902:186).”
Fowke (1902:186) described surveying the small circle at the Liberty site as follows: “Stakes were set 100 feet apart along the middle line of the embankment, beginning at the south side of the gateway. The bearing of each stake was then taken from the one next preceding. …[T]hey read as follows: 21° 35’, 3° 09’, 20° 31’, 4° 45’, 10° 44’, 17° 16’, 17° 37’, 11° 35’, 18° 35’, 14° 43’, 13° 54’, 19° 28’, 13° 13’, 17° 18’, 14°29’, 7°30’,2° 36’, 5° 57’, 25° 19’, 19° 01’, 12°55’, 8° 48’” (Fowke 1902:186). This passage provides insight into their data collection, demonstrating a precision of a minute of arc.
Hively and Horn (1982:S7, Table 1) reported on resurveying the Newark Octagon site (33Li10), a Hopewell earthwork that Middleton and Fowke had also examined. Their eleven test lines differ in azimuth from the 1880s data by an average of 18’, or by 13’ if the single greatest error is eliminated. It is difficult to assess what these data imply, because we know the veracity of neither survey. I am uncertain of the surveying ability of Hively and Horn, and am unable to comment on their level of experience at that task. One assumes that Middleton and Fowke were practiced surveyors inasmuch as that they were hired by the Smithsonian to perform the duty, albeit with equipment a century older. However, Hively and Horn also used an optical surveying transit, not a laser-based total station.
Hively and Horn (1982:S7) estimated the error range or accuracy of the Middleton/Fowke data as +/-15’, or plus/minus a quarter of a degree. This seems plausible, as their own results differed by about that much for each azimuth when compared with the older figures. However, we remain uncertain as to how accurate either survey is with respect to the actual earthwork measured. If a total station were used today at the Newark Octagon, the best preserved of the Hopewell sites, we would then have a benchmark for assessing the accuracy of the 1880s azimuths. Similar detailed assessments could be made at other sites where geophysical surveying (e.g. ground penetrating radar and magnetometry) has been employed.
In lieu of these options, let’s instead assume that both surveying teams, Hively and Horn and Middle and Fowke, collected data of equal accuracy. In such a case, we could assume that the true azimuth value for an earthwork embankment would lie midway between the respective figures from each survey. The working mean difference between the azimuths measured in each survey as mentioned is 13’. Halving this difference would yield the mean error for each survey by this model. This halved value would represent the accuracy of each survey, stated as an error range (i.e. +/- 6.5’). Considered in this manner, the uncertainty value for the Middleton/Fowke data would be +/- 6.5’, not the +/- 15’ range suggested by Hively and Horn.
I think the +/- 6.5’ figure is appropriate. Middleton and Fowke regularly cited their data to the nearest minute of arc. Fowke as quoted above noted the care with which he and Middleton performed their measurements. It is impossible to imagine a trained surveying team regularly entering azimuth errors in the 6’ range. However, this value of 6’, which is 1/10 °, is equal to a one-foot error at 575 feet in the field. The embankments at Liberty are in the 450 to 500+ foot range. Middleton and Fowke did not use the 100-foot chain to measure each embankment. Instead, they sighted along the embankment ridgetops and stood at each corner of the square where these sightlines converged. Distances between these corners are about 1110 feet. It is easy to imagine them placing and sighting the flag with a one-foot error. Note though that Hively and Horn used the same method as Middleton and Fowke, so that their data would also face similar limitations. As such, the +/- 6.5’ ≈ +/- 0°.1 error range (in azimuth) is the best we can do when relying on these surveys.
The Middleton/Fowke data (Thomas 1894) were presented in two ways when they were published: first as tabular figures, and second as plats (Figure 2). Some of these plats have errors. For instance, the connecting avenue at the High Bank earthworks is shown too wide (Thomas 1894:477. Plate xxxvii), defined by the wrong survey station in the plotting of its width. Such errors are, however, random errors, not systematic errors.
 I am able to geo-reference these plats into an Arc Map program. The proportions of the earthwork on the plat when measured in this GIS application match the Middleton/Fowke survey data. The square can be georeferenced in Arc Map so as to match the best fit to the survey distances and embankment azimuths without distorting the plat. This process yielded an accuracy to within 0°.1 for any azimuth. As such, I am satisfied that the survey data and the plats from Thomas (1894) are in very good agreement.
Robertson (1983: Table 2) lists the accuracy of the Middleton/Fowke Liberty square plat as one-degree. This error is correct as regards the north arrow drawn on the plat: it is off by about a degree. This again is a random, not a systematic error, and in any case it does not effect the internal consistency of the azimuths between the gateways as defined by the plat. (The erroneous arrow is not used in georeferencing the plat. As noted, plat orientation is based on matching the Middleton/Fowke data as regards the azimuths of the sides of the square.)
Considering my own results at Hopeton, and Hively and Horn’s work at Newark and High Bank, it appears that the Hopewell used sightlines that were defined by the termini of the embankment walls. Stated in another way, they used the edges of the gateway openings as backsights and foresights. A typical Hopewell geometric enclosure has gaps at the corners or along the walls of the various polygons, typically at the mid-point of the embankments. These gaps are called “gateways”. Hively and Horn  showed  that an embankment at the Newark Octagon was shortened in a direction away from geometric symmetry, effectively widening the attendant gateway, and that the gateway edge so-defined by the shortened wall forms a precise foresight for a lunar sightline (1982:S14) (Figure 3).
Many of the gateways at the various enclosures have widths which differ greatly from one to the other. According to my analysis of the Liberty earthworks, virtually every eligible gateway edge serves as either a backsight or a foresight for the various sightlines (Figure 4). At Hopeton, the gateway that marks the backsight locus for the winter solstice sunrise was made narrower by an extension of the tapering embankment terminus (Figure 5). Clearly, the method of defining azimuths at these sites involved gateway-to-gateway sightlines, not the ridgelines of the embankments as suggested by Hively and Horn (1982:S12-S14, Table II). Hively and Horn actually used both methods to define azimuths, but the gateway-to-gateway method supersedes the reliance on embankment ridgeline azimuths, because the former method can reproduce all of the sightlines delineated by the latter, but not vice versa.
Ultimately, and most importantly, the Middleton and Fowke data provide results that are consistent with on-site sunrise observations. In 1983, I calculated the calendrical sightlines for the Hopeton earthworks using the 1880s survey data. Then in 1998 (Turner 2011), I confirmed the accuracy of those resultant azimuths at sunrise and sunset in situ at the earthwork. So while it may be impossible to cite a precise value for the accuracy of the Middleton/Fowke survey data as such, the figures are certainly true enough to yield testable archaeoastronomical sightlines. In this regard, my present study is suited and intended to guide future researchers in testing proposed calendrical sightlines at an earthwork, and in archaeologically testing the loci of horizon foresights as indicated by those sightlines.

Data Analysis Using GIS
Hively and Horn (1982, 1984) and myself (1982, 1983) utilized essentially the same method in our investigation of earthwork sightlines. We were limited to using paper maps and hand calculators. Aerial photographs of the earthworks were projected and traced onto USGS 7.5’ topographic quadrangles in order to accurately position them for analysis. I used a millimeter ruler and jeweler’s loupe to measure sightline features on the USGS maps. With these now outdated methods, I obtained accurate results that were confirmed by on-site observations of solar events (at Hopeton). So it is with greater confidence that I attempt to execute the same process using GIS software.
An Arc Map document is created. I use DRG files of the USGS 7.5’ quadrangles. For representation of terrain, Digital Elevation Model (DEM) files are uploaded and geocoordinated to the data frame (CITE). Scanned JPG images of the Thomas (1894) plats can then be georeferenced into the layers. Shapefiles are used to represent and manipulate polygonal, linear and point data.
The location of the Liberty earthworks can be established using the map published by surveyor James Marshall (1987:41, Figure 3b). The scale is low, but the map allows for the rough placement of the earthwork. Then, so guided, the outline of the square (and the small circle) can be seen in the Lidar-based DEM when converted to hillshade in ArcMap  (Figure 6). In this view, the northwest and southeast sides of the square are the most visible, especially so the latter. The northeast side is the most poorly shown, but it too is visible in part.
The most visible sections of wall are about 50 feet in width as measured in ArcMap. The midline of these embankments is easy to determine, and is probably accurate to no worse than +/- 5 feet. Note that this uncertainty in positioning the square on the landscape does not effect the azimuths as determined from the Middleton/Fowke data. Those data and the geometry that produces them are internally consistent within the square itself. The shift of +/- 5 feet does however effect (by that amount) the loci of any horizon foresights that are plotted.
As a check on this method of siting the square, its dimensions after being georeferenced can be compared with those cited by Middleton and Fowke. The size of the plat can then be expanded or contracted on a fine scale to match those survey data. Furthermore, the ArcMap editor tool COGO has functions that yield the azimuths of line features on the map. This is invaluable in fine-scale georeferencing the plat to match the 1880s data, and in quantifying subsequent azimuths that are being tested as calendrical sightlines.
I had already analyzed the Liberty square fifteen years ago using the paper map method. The paper from then has remained unpublished, but the current text uses sections of it. Data from the results of that study allowed for initial placement of suspected sightlines into the ArcMap format. I was then able to test and render more precise the predicted sightline azimuths and the loci of the associated horizon foresights.
In these analyses, it is necessary to know the elevations of the backsights and foresights, the endpoints that define each complete sightline. Because the horizon foresights are typically along a ridge or at a mountain peak, the resultant differences in elevation produce an angular horizon height as seen along each viewline. This horizon altitude in degrees of arc is an important factor in the spherical trigonometry calculations employed in archaeoastronomical research. Using USGS 7.5’ topographic maps Hively and Horn and myself measured and calculated this factor for all of our sightlines. Others do not, but rather use approximation tables (Romain 1991).
When using paper maps, estimates for site elevation are made as based on nearby lines of elevation contour, and are probably good to 5 feet in the z-axis. ArcMap provides much finer grained elevation values, especially with the use of Lidar-based DEM data. The ID function in ‘data view’ provides point elevations with a precision far exceeding the first decimal point in meters or feet. GIS allows for the production of highly precise data such as these, yielding a more accurate result after their insertion into the archaeoastronomical algorithms.
It is appropriate here to discuss the equation used in making these calculations. It is as follows:
sin δ = (sin Φ sin hc) (cos Φ cos hc cos A)
where
Φ = site latitude, easy to determine with great precision using ArcMap
A = azimuth, the bearing of a proposed sightline
δ = declination of location in sky marked by sightline. This is the resultant factor of the equations, the figure which denotes celestial significance or not
hc = corrected horizon height. This factor is the most complex. It is based firstly on the true horizon height as dictated by the skyline itself in any given direction. This true horizon height, h0, is then modified by three attendant factors, such that
hc = h0 –  r  +  p   +/- q
where
h0= true horizon height
r = atmospheric refraction
p = parallax (of sun or moon)
q = semi-diameter (of sun or moon)
where q = -0°.26 first/last gleam of the rising/setting sun or moon
or q = 0° bisection of disc of sun or moon, rising or setting
or q = 0°.26 last/first tangent of rising/setting sun or moon

h0 = the true angular height or horizon altitude along a given sightline.
r   = the atmospheric refraction value, which varies with the horizon altitude. The lower the horizon, the greater the apparent displacement of the celestial object located there. This displacement amounts to 0°.58 for a zero-degree horizon. It is 0°.41 when h0= 1°.0. A specific r-value must be inserted for each unique h0 value (see Thomas and Joseph 1996).
The parallax value is an artifact of the trigonometric method. The spherical trigonometry model used is calculated from the center of the earth with respect to other celestial objects. But we are on the surface of the earth, about 4000 miles from its center. This displacement has no effect when calculating the locations of stars, because they lie effectively at infinity. Even the distance to the sun renders the displacement nil, the p-value for the sun being only 0°.002. The moon however is close enough to undergo a positional shift due to the 4000-mile displacement. The mean parallax value for the moon is 0°.95, or about twice the width of the moon or sun.
The q-value proves to be the most problematic, and its effects are not trivial. It is easy to assess the misuse of the r-value or p-value by researchers, but the handling of the q-value can be more subtle. The q-value represents which phase of the sunset is observed or mathematically modeled. There are three phases. One, we can note the first gleam of the rising sun or moon. Two, we can note the central bisection of the disc, i.e. the sun or moon half-risen. Or three, we can note when the solar or lunar disk is just touching the horizon, the so-called tangent event. The order of these three events at sunrise is first gleam, half-disk, tangent. The order is reversed at sunset, but the effect is the same. Any given declination result which we calculate will be about 0°.4 further north for gleam events than for the tangent events. This 4/10 degree is no trivial sum, considering that the moon and the sun are each about 5/10 degree in diameter.
Misuse of this range obtained by changing the q-factor to “fit” the sightline is a methodical error. Regarding their analysis of the High Bank earthworks, Hively and Horn wrote “We have adopted the criterion of lower limb tangency to define the rise and set points of the sun and moon. This criterion was chosen because it gave a consistently better fit to the most likely astronomical alignments” (1984:S93). However, with their earlier research on the Newark Octagon (1982:S12), they chose to use the first gleam event: “We have defined the rising point of the azimuth of the first gleam where the moon’s leading edge just comes over the horizon…”. More recently in 2013 (pp. 85-86) they utilized the tangent event, i.e. q = +0°.26, saying “it gives a slightly better fit to the data”, and that the outcomes of the analysis are “...not significantly effected.”
 In my 1983 article on Hopeton, I listed resultant declinations for all three q-values for each sightline, thus avoiding any bias, but reducing the precision of the declination value by citing it as a range instead of as a figure.
The best policy with these data is to cite the q-value in the least presumptuous way possible, with q= 0°, i.e. for central bisection of the disk, half-risen or set. This way, even if the Hopewell calendrical specialists observed the gleam or tangent phase, any resultant declination error could not exceed 0°.2.
In any case, we cannot know specifically which phase of sun or moon rise the Hopewell observed, and the landscape and associated archaeological resources are today of compromised integrity. As such, it would be difficult to reverse analyze a sightline and deduce which phase (q-value) of the sunset was prehistorically monitored. Arguably, the first gleam event would be the most salient of the three rising phases. But horizons can trace complex profiles, an array of gaps, peaks, and slopes (Figure 6b). The slope of a mountain on the horizon may parallel the edge of the rising sun and be utilized indexically as a foresight, rendering a specific q-value meaningless. The horizon gap between Bunker Mill and Mt. Ives forms a complex notch profile as seen from the Hopeton earthworks at winter solstice sunrise (Turner 2011:211, Figures 7,8,9), so that “q” yields only a best fit approximation. Monumental architecture located at a horizon foresight could block a rising sun, micro-indexing the phase, again obviating the q-value. Parsimoniously, in this present study, I am exclusively using the q-value  = 0°. Then following the analyses, all sightline horizon foresight and horizon profile terrain features are inspected in ArcView and examined regarding any noteworthy indexical characteristics.

Concerning the Calendrical Sightlines
In analyzing the Liberty square, I am guided by earlier studies. Regarding the calendrical events for which we test, we can look to the earliest Hopewell archaeoastronomy research, and see which phenomena are being suggested as celestial sightlines. The earliest of these, Eddy (1977), suspected that the Newark Octagon was “aligned” to the north lunar maximum rise, and subsequently Hively and Horn (1982) tested and confirmed his probative and pioneering observation.
Another early voice, Stocker (1981) claimed to have witnessed the summer solstice sunrise at the Fairground Circle (also called the Great Circle) in Newark, Ohio (33Li10)(Figures 8a, 8c). I went to Newark in 1982 to survey the Octagon and the Fairground Circle; to verify the claims of Hively and Horn, and that of Stocker. While there surveying the Fairground Circle, I met a local couple, Mike and Lyn Van Dorn. They assured me that the sun rose through the singular gateway of the enclosure in early May, not on June 21 as Stocker had written. They estimated around May 7th. My curiosity heightened, I reduced my surveying data upon returning to Washington DC and found that the Van Dorns were correct. My analysis revealed that the sun rose centrally through the circle’s single gateway on May 4, with the sun at half-disk (i.e. with q = 0°)(Turner 1982).
It became evident that Stocker (1981) had fabricated his account, even specifically claiming to have observed the sun ascending over the on-site museum at dawn on solstice. “On the solstice the sun rose over the museum and the following day just to the south of it, but in the opening.” Here he asserts that he saw the sunrise the second morning also, the sun having moved to the right in azimuth. In fact, the sun does not move with respect to its risepoint for about 4 days at solstice, but Stocker did not know this, and in trying to sound authoritative, he revealed his forgery.
Overall, the data show that the sun rises nowhere in the gateway at the Fairground Circle on summer solstice. Having no knowledge of these celestial motions, Stocker wrote that he “suspects that the sun rises in this opening for a four or five day period around the summer solstice.” It does not, but had the gateway axis been targeted at the solstice rise point, according to my calculations the sun would have risen within the opening for about 80 days,  not “four or five” as Stocker speculated.
This episode with the Stocker data is a stain on Hopewell archaeoastronomy. Yet this fabrication remains: I recently heard an archaeologist from Cahokia Mounds State Park give a talk on archaeoastronomy and repeat Stocker’s claim: that the Fairground Circle sightline indexes summer solstice sunrise, which it does not. All of this is problematic. But in addition, and lost in the welter, is the question: what is the correct “alignment” at the Fairground Circle?
In 1982, my immediate response to learning about the Stocker fabrication was to mail a letter to his editor at Archaeoastronomy, reporting my survey and calculation results and comparing them to Stocker. My letter was published with a data table (Turner 1982). In it, I correct Stocker’s solstice claim, and present the correct azimuths and associated declinations as seen through the Fairground Circle gateway. I broach the topic for the first time that Hopewell calendrical practices may have involved the monitoring of the cross-quarter dates.
At that time in 1982, I was already analyzing the Hopeton earthworks (33Ro26). Following the example of the cross-quarter results at Newark, I tested for cross-quarter sightlines at Hopeton. I found that the sightlines defined by the north and south sides of the Hopeton enclosure index the May cross-quarter date sunrise (Figure 7). Hence not only are these sightlines present at Hopeton, but they orient the entire large geometric outline of the enclosure on the landscape (Turner 2011).
Other researchers have asserted that the sightline at the Fairground Circle indexes the lunar minimum risepoint, even though it is about three degrees in azimuth from that event. Hively and Horn (1982:15) even suggested that the very short entry walls at the gateway index a sightline that is “within 0°.9 to the minimum northern extreme rise point”, a claim they later retracted (2013: 96)(Figure 8b).
In the same articles they acknowledge that the axial sightline at the Fairground Circle misses the north lunar minimum rise by more than three degrees. In 1982 they wrote “A line from the center of the circle to the center of the avenue misses the lunar risepoint by more than three degrees” (page 15). Keep in mind that Hively and Horn usually would not take note of a sightline with an error of three degrees, nor would anyone, let alone consider it. Yet again in 2013, they persist with this interpretation, writing “the best that one can say” is that the sightline “points in the general direction of the northern minimum extreme moonrise (within 3°)” (page 97).
Hively and Horn (2013:96) also attempt to cast doubt on the possibility of determining an accurate sightline azimuth at the Fairground Circle. They assert that the location of the center of the enclosure, and hence the location of any proposed backsight, is imprecise because of the irregular outline of the circular embankment. The Fairground Circle is irregular as compared to the nearby Observatory Circle, but using ArcMap and the Middleton/Fowke data, it can be shown that the geometric centroid of the circle and the Eagle Mound-to-gateway axial sightline are separated by less than three meters (2.46 m)(Figures 8b, 8c, 8d).
Additionally, Hively and Horn suggest that the relatively short entry walls that flank the gateway entrance somehow compromise the observation of an accurate axial sightline azimuth as seen from the center of the great circle, which is certainly not the case (Figure 8b).
In truth, there are few Hopewell enclosures if any whose effective working centers are as easy to locate as that found at this site. Not only is there a set of low mounds marking the location (the Eagle Mound), but a structure stood there in Hopewell times. Subsurface postmold patterns indicated a long narrow design with the axis toward the gateway (Greenman 1928, 1929)(Figure 8b, 8c). It would be difficult to define a more precise backsight locus than that found with this prehistoric structure, and it is the only such structure known at a Hopewell enclosure that is situated at the locus of a calendrical backsight.
The Hively and Horn assertion that the Fairground Circle gateway lacks symmetry and axiality is also specious. The entry causeway is extremely well defined in width, its boundary formed by the edges of the interior ditch or moat. Measurements or sightings defining axiality can be easily and accurately made in situ or on maps. Overall, there are many indices of axiality available, and it is not problematic to measure an axial bearing when surveying at the Fairground Circle. I always obtained consistent results when doing so (Turner 1982).
Romain (1995:48) mistakenly interprets Hively and Horn’s Fairground Circle results. Romain states that these earlier researchers had reported finding an accurate lunar index along the axial sightline, which they did not claim, as noted above. They reported an error of more than three degrees. Romain blithely asserts that the axial sightline correctly indexes the north lunar minimum rise, ignoring the three-degree error.
Amidst all of this misinformation, my attempt to call attention to the possibility of the Hopewellian observation of the cross-quarter date has been unsuccessful. Yet the Fairground Circle poses a unique question. It possesses only one sightline, unlike all of the other more complex Hopewell geometric enclosures. Either the sightline points to something of celestial significance or it doesn’t. It does not index summer solstice as Stocker averred. It does not pinpoint the risepoint of the north lunar maximum moon rise. It does mark the location of sunrise at the May cross-quarter date. This is sufficiently compelling, so that when I investigate other Hopewell sites, I will now test them for cross-quarter sightlines.
As stated at the beginning of this section of this paper: “In analyzing the Liberty square, I am guided by earlier studies. Regarding the calendrical events for which we test, we can look to the earliest Hopewell archaeoastronomy research, and see which phenomena are being suggested as celestial sightlines.”

The Liberty Earthworks: Prior Research
Hively and Horn (1982:18) commented briefly on the Liberty earthworks, saying only that “some kind of astronomical orientation” probably existed. Romain later analyzed the Liberty square (1991). His is a good example of the type of results obtained when using approximation tables in making calculations and when using plastic overlays in determining sightline azimuths.
In his analysis, Romain utilized approximation tables, effecting the precision of the variables horizon altitude and geographic latitude. Romain’s errors arise in part from his fixing all sightlines to a horizon altitude of one-degree. In my own analysis of the Liberty square, I have found h0 values ranging from +0°.7 to +1°.9. Changing h0 by 0°5 results in a change of declination of 0°.4. Also, Romain arbitrarily chose to use a q-value of +0°.26, that used for the tangent phases of the rise and set events of the moon or sun. As mentioned earlier, this factor accounts for a change in declination of two-tenths degree relative to using a q-value of zero (bisection of the disk). Romain’s azimuth data are created using plastic overlays scribed with lines. These factors all combined to yield to a level of inaccuracy that Romain acknowledged, stating that the resultant error range is “probably no more than plus or minus one or two degrees” (Romain 1991:4).
Indeed those were the results I found in examining his sightlines. Of the six sightlines he postulates for Liberty (all lunar)(Figure 9), all miss the proposed lunar extrema declinations by 1°.0 to 1°.7. That is to say, these sightlines would miss the correct rise or set points by two or three moon widths, rendering them ineffectual. I analyzed Romain’s listed azimuths (1991:12) using an Excel spreadsheet modeled to handle all of the variables as listed earlier. Following Romain’s method of analysis, I set the q-value to +0°.26, horizon altitude to one-degree, and the parallax to +0°.95, appropriate for the lunar events suggested by Romain (see Table 1).
Romain (1991: Figure 4) drew his sightlines on a plat of the Liberty earthworks from Thomas (1894). I georeferenced his diagram into Arc Map and used the COGO editor to measure the azimuths of the proposed sightlines. I have georeferenced the Thomas plat in ArcMap to a concentric azimuthal accuracy of 0°.1. Hence I have confidence in this method of measuring Romain’s lines.
Romain (1991: Figure 4) lists azimuth figures in conjunction with the diagrammed sightlines: but these azimuths do not match those of the lines. For instance, sightline C – D is listed as having a bearing of +53°.2, but it is actually +51°2 as diagrammed on his plat. When the listed azimuth values are plotted as sightlines, they “hit” the embankments and do not go through the gateways (Figure 10).
What is achieved by noting sightlines whose error range is +/- 2°? If we allow that the Hopewell geometric earthworks  were used prehistorically to establish and monitor calendrical sightlines, we can assume then that the technology associated with indexing the motions of the sun and moon would have developed over centuries, and that the calendrical specialists would have developed sightlines of much finer precisions and accuracies than is suggested by the +/- 2° figure. By presently analyzing the Liberty square with regard to high-precision sightlines, I am striving to provide precise positional data that can be used by future archaeologists in examining horizon foresight loci. With high-precision sightlines, researchers using ArcMap and ArcView can examine specific horizon foresights such as mountain peaks, gaps, or other associated terrain features. When we find a sightline that utilizes landscape features as specific as peaks or gaps, we then have corroborative evidence that the sightline was intentional, and it allows for a very accurate plotting of the foresight locus on the topographic map, or in finding the foresight locus in the field.
With low-accuracy sightlines, such subsequent analyses are impossible. High precision data afford the best opportunity for hypothesis-testing the intentionality of proposed calendrical sightlines. By use of geophysical surveys and excavation, archaeologists can note the presence of cairns, FCR concentrations, ritual deposits, or any other evidence of practices associated with Hopewellian horizon foresight use.

Analysis of Calendrical Sightlines
My analysis showed 17 total sightlines. Two of these are equinox lines that have declination errors of about 0°.7 and 1°.0. Of the remaining accurate 15 lines, four sight equinox, six mark cross-quarter events, and five index lunar phenomena. Rising and setting events are equally represented among the solar lines. However, of the eight possible horizon azimuths associated with the lunar maxima or standstills, only three are present in the resultant data
Several points are notable concerning the Liberty square analysis. First is the presence of cross-quarter date sightlines. These have been previously found in a Hopewell context at the Fairground Circle (Turner 1982, 2000) and at the Hopeton earthworks (Turner 1983, 2000, 2011). Based on my own unpublished calculations, they are not present at the Baum earthworks (33Ro4), nor at the High Bank group, nor at the Newark Octagon. The finding of cross-quarter sightlines at Liberty supports the interpretation that these sightlines were subsistence scheduling indices used by the Hopewell with regard to horticultural food production (Turner 2000).
There is an absence of solstice sightlines at the Liberty square, but equinox is indexed for both the rise and set events, with multiple lines in each direction. Some of the paired equinox and cross-quarter sightlines make use of the same backsight locus. This means that an individual standing at this locus could observe sunrise at and between March 21 and May 4 and monitor the date during this period with relative precision. This segment of the calendar year brackets the germination and planting phase of the spring season. The use of day-counts at this time of the year would already be implicit in the determination of the cross-quarter date. A detailed schedule of subsistence related practices could be easily developed using day counts during the interval between equinox and the May cross-quarter date (Figure 10b).
Summer and winter solstices are highly salient events and the most frequently observed events prehistorically, yet they do not figure importantly as regards horticultural scheduling (Hardman and Hardman 1992). The May cross-quarter date is of prime importance in this regard, and the success or failure of its timing poses the greatest overall risk to food production goals. These combination equinox and cross-quarter backsights found at the Liberty square may have resulted from 1) practices developed with the intensification of the Eastern Agricultural Complex during the Early and Middle Woodland periods (Braun 1987, Smith 1992, Turner 2000) and 2) a co-evolving Hopewellian subsistence scheduling regime with its associated observational technology and calendrical knowledge .
As regards the lunar sightlines, these number only 5 out of 17 total sightlines. Among the rising events, only the south lunar minimum is marked. Lacking are three other lunar rise events. For instance, the lunar maxima are not indexed. The lunar maxima are more observationally salient than are the lunar minima, and we would expect to find these first. Among the setting events, we find the lunar minimum north and the lunar maximum south lines represented.
None of these lunar sightlines are mirrored by their normally paired opposites. That is to say, there is an accurate south lunar maximum set line, but no north one. Nor is there a south lunar maximum rise line.
There is an accurate north lunar minimum set sightline, but no south one. Nor is there a north lunar minimum rise line. These facts call into question whether these lunar alignments were intentional or merely structurally coincident. Such possibly superfluous lunar angles are present at Baum (Turner, unpublished data, 1982), where the solstices are repeatedly delineated with just two lunar set sightlines possible. By contrast, at Hopeton (Turner 1983, 2000), High Bank (Hively and Horn 1984), and the Newark Octagon (Hively and Horn 1982), all four lunar extrema are indexed for both rising and setting events, sometimes with multiple sightlines.

Problems with Defining the Date of Equinox and Cross-quarter
The two solstices are exactly definable in the annual cycle, even to relatively primitive observers (Duncan 1998). These are the extreme angles north and south to which the sun travels in the sky. Besides changing the length of the days and giving us our seasons, the positions along the horizon at which the sun rises and sets reach their greatest points north and south. At these extremes, the azimuth of the rising (or setting) sun at either solstice essentially does not change for a four or five day period. The word solstice means “sun still”. Hence the Hopi say that the sun, Tawa, “rests or dances” in his “house” (location along the horizon) during the four-day interval.
Because of this lack of motion, these horizon points are relatively easy to define observationally. If cloudy on one or two mornings, there are still a few more days to witness the event.
The exact opposite is true at equinox. At these times of the year (ca. Sept 21 and March 21), the daily rate of change of the horizon rising/setting points is at its greatest. It amounts to about the width of the sun’s visible disk per day at the equinoxes. Brief cloudy weather can easily ruin the chance to observe this event (rise or set). Additionally, the rate of change of the sun's position is so great that the diurnal hour of equinox (which changes year to year) may not coincide with the hour of sunrise (or sunset). Hence it is impossible to define an exact azimuth indexing the event, quite the opposite of the solstice observations.
Further uncertainty in defining the day of equinox comes from the shape of the earth’s orbit, which is not perfectly circular. As per Kepler’s laws of orbital motions, the earth is traveling faster when nearer to the sun, and slower when further. These near and far points in the earth’s oval orbit are called the perihelion (near point) and the aphelion (far point). These occur yearly in early January and early July respectively.
It is for this reason that the two halves of the year as viewed geometrically are not equal temporally. Specifically, winter in our hemisphere is about 4 days shorter than our summer. This inexactitude introduces further difficulty in defining a precise day for the equinox (Fletcher and Cameron 1988:57; Hardman and Hardman 1992:153, Ruggles 1999).
Astronomically, equinox can be defined to the hour (or even the second) as the moment when the sun passes over the earth’s equator. On this day the sun is said to rise due east and set due west. This also however is an approximation. Because of atmospheric refraction and varying height of each observer’s local horizon terrain, the azimuth of the rise or set point is altered,  increasing in azimuth as horizon altitude increases, so that it is incorrect to say that the sun rises exactly and uniquely due east on equinox. This definition of equinox (sun rising due east) is therefore not valid either.
One is left with the approach of counting days between solstices and halving the amount. Prehistoric American Indians may have used knotted ropes or pebbles to record and manipulate such ordinal and interval data. Ethnographic accounts of notched sticks are also well known. So-called calendar sticks have been noted in a Pueblo Indian context (Zeilik 1985). The Winnebago calendar stick as documented by Marshack (1985, 1989) gives clear proof of Native American numeration abilities. Accounts of California tribes demonstrate similar methods (Hudson 1984, 1988; Hudson et al 1979).
To illustrate day counting with an actual example, consider the March (vernal) equinox 1999. The vernal equinox occurred on 21 March, 2 hours UT (Universal or Greenwich Mean Time). By contrast, the temporal halfway point between the prior and following solstices, that which would be obtained by counting days and halving the amount, was at 22 March, 23 hours UT. Thus the equinox as based on a daily tally differed from real equinox by 1 day 21 hours.
The sun’s declination at this point was not zero degrees, as defines true equinox, but rather + 0 45’. Again, this occurred nearly a full two days after vernal equinox. A similar effect was had in September 1999, when the “temporal” equinox occurred 1 day 22 hours before true autumnal equinox. Hence the azimuths of sunrise at the equinoxes based on day-counts is north of the sunrise on the true equinoxes.
Remembering that the sun’s daily motion is so great at these times of the year, it becomes apparent that pinpointing an exact location for the sunrise which defines the equinoxes is essentially impossible. One would expect to find multiple sightlines indexing these horizon loci, but with a span of a few degrees, likely off center to the north (Hardman and Hardman 1992:165). Such repeated equinox lines are found at Hopeton (Turner 1983, 2000) and as they are at the Liberty square. On the ridge to Hopeton’s east, just north of these sightline foresights, lie some burned sandstone outcroppings that may have served as sightline indices for the “day-count” equinox (Turner 1983, 2000).
Given the difficulties of determining an observationally plausible equinox, the placement of the cross-quarter dates is even more ambiguous. The cross-quarter dates occur midway between the solstices and the equinoxes (McCluskey 1989). They were observed as agricultural/ritual events in prehistoric Britain and amongst the Hopi. Due to its timing as a safe and practical planting date, the May date is the most important of the four cross-quarter points. It was called Beltane, and later simply “May Day” in prehistoric Britain (James 1961). The Hopi call it neverktcomo (Forde 1931:384) and place it as May 3rd. It is indexed by the Hopewell Fairground Circle (Turner 1982, 2000) and Hopeton earthworks (Turner 1983, 2000, 2011).
As with the equinox, and for the same reasons, the date of “May Day” is difficult to define exactly. Differing dates are obtained depending on whether one considers a geometric halving of the seasons, a temporal division, or even as based on the celestial longitude (right ascension) of the sun. There are no unique salient celestial cues that would suggest a date to a pre-modern observer. The cross-quarter sunrise azimuth is not located midway between the azimuths for equinox and solstice along the horizon. The sun’s path through the sky is described by a sinusoidal curve, so that this medial azimuth occurs around April 21. Also, whereas the solstices always occur at precise horizon loci, and the equinox sunrise will always be close to due east, no obvious azimuths defined by the north-south-east-west grid exist for the cross-quarter dates. Hence, evidence of their indexing as demonstrated by calendrical sightlines is even more suggestive of the counting of days than is the case with equinox. Accurate scheduling of the cross-quarter dates inescapably requires day counting.
McCluskey (1989:S3) lists the solar declinations on the cross-quarter dates as based on the various models mentioned above. He obtains a range for “May Day” of about 6/10 of declination. This corresponds to a three-day period at this time of year. Additionally, depending on whether an observer is watching for either the first gleam of sunrise (q = -0°.26) or for the entire solar disk to clear the horizon (q = +0°.26), another two days is introduced into the time span.
[Note: Since Hopewell times two millennia ago, the inclination of the axis of the earth has shifted, lessening by about 0°.2. Today’s value is under 23°.5, whereas circa AD 1 it was 23°.7. This is why when we look for Hopewell solstice sightlines we test for the latter, not the former figure. Equinox is unaffected. Because of this change in inclination, if a specific cross-quarter declination was being monitored by the Hopewell two-thousand years ago, this declination value would be reduced by about 0°.1 today. So while we do correct for this shift in our solstice calculations, given the uncertainty in knowing a precise value of declination for cross-quarter date, the effects of the change in the earth’s inclination with regard to indexing these sightlines are nearly nil and essentially unobservable.]
All told, therefore, the May cross-quarter date can be said to occur sometime from May 3rd to the 7th. Given this ambiguity, it is difficult to assign a unique declination when defining the cross-quarter dates. If indeed the Hopewell were monitoring the cross-quarter event, we can look to the two other known examples at Hopeton and the Fairground Circle for insight. What declination is indexed by the cross-quarter sightlines at these earthworks?
This is especially important with regard to the Fairground Circle. Only one sightline exists there, and contrary to what Hively and Horn assert (2013:96), it is easy to determine with high precision. Not only are the backsight locus and foresight gateway well defined, additionally there is a salient horizon foresight feature at the terminus of the sightline (Figure 8g).
As mentioned earlier, Greenman excavated the Eagle Mound at the center of the Fairground Circle in 1928. He discovered a series of postmolds in the mound floor, but the map of these has never been published (Greenman 1928). Additionally, the precise locations of these postmolds are uncertain. Greenman plotted them with reference to the outline of the Eagle Mound. During excavation, he leveled this mound, and reconstructed it afterward. Our data with regard to the precision of the postmold loci are the reconstructed mound and a hand drawn site map. It seems reasonable to suggest that the mound was reconstructed with no more than five feet error in its location.
We know from Greenman’s map that the postmolds were under the main body of the mound, which has four lobes or subsections. The postmolds appear to occur in two groups. Under each of the smaller side lobes of the Eagle Mound, particularly the northern one, there was a series of postmolds in a line angling away from the main axis of the mound. The remainder of the postmolds are under the axial portion of the mound, primarily under the highest section of it. The rectangular layout of these postmolds conforms to the outline of a structure about 48’ by 22’, with the long dimension in line with the sightline to the gateway center. Because its width is 22’, a five-foot uncertainty in the postmold loci would still place the backsight of the sightline within the outline of the structure. A shift of five feet at the backsight perpendicular to the sightline causes a shift in sightline azimuth of only 0°.03, with a corresponding shift in the indexed declination of 0°.02. Hence the suggested five foot uncertainty in backsight locus is acceptable for sightline analysis, and does not render the determination of the azimuth inaccurate.
In conjunction with the present study, I reanalyzed the Fairground Circle sightline and the Hopeton cross-quarter sightlines using ArcMap and Excel. The Fairground sightline for sunrise indexes the declination of +15°.6 with q = 0° (bisection of disk). For the Hopeton sightlines 1-11 and 5-7 the declinations were +15°.6 and +15°.5.
Both of these Hopeton sightlines are associated with terrain features at the horizon foresight loci. Sightline 5-7 terminates exactly at the gap saddle between Bunker Hill and Sugarloaf Mountain, an easily noted horizon feature as seen from Hopeton. The 1-11 sightline ends at a flattened area along the northeast ridge of Bald Hill.
I field surveyed these ridges in 1982, and noted a thirty-foot in diameter sunken circular area at this latter foresight locus. I was able to find this flattened section of ridgeline using ArcMap. A one-foot contour map was made from a high-resolution LIDAR-based DEM. The flattened area of the ridge was easily found and it was exactly where my field notes from 1982 suggested: about 790 feet or 240 meters northeast of Bald Hill knob along the ridge.
In analyzing Hopeton sightline 5-7 (see Turner 1983), a test line in ArcMap used for azimuth analysis was positioned to begin at station 5, the northwest corner of the earthwork. The line was then set to terminate at the ridgeline foresight locus noted above. The resultant sightline passed exactly at the brow of the embankment just north of the Middleton/Fowke survey station 7 (the northeast corner of the Hopeton polygon), i.e. exactly parallel with the north side of the Hopeton enclosure. This surfeit of corroborative data is exciting to say the least.
With regard to the Liberty earthworks, the cross-quarter sightlines found there can be compared to the declination value indicated at Fairground and Hopeton. This value is +15°.6. Given the vagaries introduced into our current leap year calendar, this declination corresponds to the sunrise on May 3 or 4.

Horizon Foresights
Calendrical sightlines are not only indicated by earthwork features, but also by the landforms of the natural terrain that define the visible horizon, or by the placement of mounds, rock cairns, or other structures at such loci (Turner 1983, 2000, 2011). It is possible that the sightlines at the Liberty square were intentionally “aimed” at peaks or gaps along the horizon. Such features would readily serve as azimuthal indices with regard to sunrise or moonrise. The use of these features would have predated the construction of the earthworks themselves, perhaps by centuries. These natural foresights were the initial horizon calendar indices utilized by the Hopewell. Such are suppositions allowed through operational sequence analysis and they are implicit. Any familiarity with the azimuthal variations in the sun’s risepoint along a local horizon  could occur only after sedentism had occurred.
Figure 11 shows the elevation variations in the region of the Liberty earthworks. While the earthworks lie within the relatively flat floodplain of the Scioto River, the site is surrounded by hills or low mountains, especially to the east and west, the directions of the rising and setting sun and moon.
In examining the Liberty earthworks, I tested for the following astronomical phenomena: winter and summer solstice, equinox, the cross-quarter days, and the lunar extrema or standstills, both the minima and the maxima. All sightlines are calculated with q = 0°, for central bisection of the rising or setting disk. The correct value for atmospheric refraction was entered for each sightline. Parallax was set to 0°.002 (effectively zero) for the sun and 0°.951 for the moon. Precise elevations for the backsights and foresights, derived from ArcMap using the ID tool, were used to calculate the apparent horizon height for each sightline. Sightline azimuths were determined using the COGO Report toolbar in ArcMap. All calculations were done in Microsoft Excel.
All sightlines were plotted in ArcMap and each foresight was examined for its association with any salient or otherwise notable terrain features. Maps of these sightlines and foresights are exported as JPGs and used as figures in this report.

Sightlines and Foresights at the Liberty Square
I begin by discussing the equinox rise lines. There are three of these (Figure 12). One of them is in error with respect to the idealized equinox declination of 0°. This sightline begins at gateway E, and sights through gateway F. (Note that for clarity I call this “sightline E-F”, and that I follow such nomenclature throughout.) This sightline E-F indexes the celestial declination -0°.7, hence with an error amount that is greater than the 0°.5 width of either the moon or sun.
The remaining two equinox rise lines are exactly precise for a half-risen sun (q = 0°). The foresights for these two sightlines, H-G and D-B, are less than a mile from the square earthwork (Figures 13 and 14). This is not a common occurrence for the Hopewell enclosures, where the horizon foresights are usually atop the more distant surrounding mountains or ridges. Nonetheless, these foresights are located at the highest loci possible on this nearby ridge (Figure 14).
There are no solstice sightlines (rise or set) indicated at the Liberty square. There are cross-quarter sunrise events marked, however, one north and two south (Figure 15). Line D-G sights to the declination +15°.3, when q = 0° (Figure 16). This corresponds to sunrise on May 2. This differs from that at the Fairground Circle by two days, where the sun rises axially with regard to the gateway and Eagle Mound on May 4 with  q = 0°.
The sightline D-G foresight area has been disturbed by railroad construction activity, and it is possible that the original locus has been destroyed (Figure 17). The elevation of the proposed foresight, however, appears to have been of greater elevation than the disturbed area in question, and may have indeed been the original foresight.
The two cross-quarter south rise lines, H-B and D-F, correspond with declinations of -15°.6 and -15°.5 respectively, with q = 0° (Figures 15 & 18). The sightline D-F foresight is located on a discrete and distinct peak feature, easily seen from the Liberty square (Figures 19, 20 & 21). Both lines H-B and D-F index sunrise dates in early February and early November, at two of the four annual cross-quarter dates. These sightlines if intentional mirror the northern cross-quarter sightline.
In contrast to these February and November dates, the preeminence of the May cross-quarter date is indicated by its singular indexing at the Fairground Circle. At Hopeton, the May cross-quarter rise sightlines define the orientation of the entire enclosure. There is record of the Hopi once having observed the May cross-quarter date with a horizon calendar sightline (Forde 1931:384-386). This index was used to time spring plantings. The month preceding the May cross-quarter date was called hakiton-muya, or the “waiting month”, viz: wait to plant so as not to suffer a late freeze (Malotki 1983:357, 374-377). The May cross-quarter event appears to have held preeminence among the four annual dates.
We could argue that of the four dates, the May date would be most salient, the recognition of which would occur first among the cross-quarters. Due to its agricultural importance regarding the timing of spring planting, it is the cognitive anchor which leads in some cases to the observance of all four of the annual calendar dates. If such a point is reached, the year effectively becomes divided into eight equal segments.
Last among the rising lines, this sightline also uses gateways D and F, as does also one of the prior examples. However, this line utilizes the opposite edge of the foresight gateway, and hence has a different azimuth. To distinguish this sightline, since it involves the moon, I will refer to it as “D-F lunar”, in contrast to the earlier cross-quarter south rise line “D-F”.
This sightline, D-F lunar (Figure 22), is the only rising event involving the moon. It marks the south lunar minimum risepoint (with q = 0°, δ = -18°.6). However, there are no lunar maximum rising events at the Liberty square, neither south nor north. Nor is there a corresponding north lunar minimum rise line.
By comparison, the Hopewell geometric enclosures that are known to have lunar sightlines each index the entire suite of the extrema azimuths, often with multiple redundant lines. These sites include Hopeton, High Bank, and the Newark octagon. Each of these sites indexes all eight of the lunar extrema: north and south lunar maximum rise, north and south lunar minimum rise, north and south lunar maximum set, and north and south lunar minimum set.
Additionally, the Newark octagon, the most geometrically regular polygon of the three, excludes all solar sightlines in its design (Turner 2004). A distorted octagon, the High Bank earthwork indexes all of the lunar extrema, and all four of the solstice events: winter solstice rise and set, and summer solstice rise and set (Hively and Horn 1984). Hopeton is the least regular of the three, and although it too indexes the lunar extrema and solstice events, in addition equinox and the cross-quarter dates are also marked by its sightlines (Turner 1983).
The equinox and cross-quarter azimuths are not indicated at either the Newark octagon or at High Bank. They are present at the Liberty square however. If we accept that the Hopewell enclosures were indeed used for these calendrical observations, we must accept that these apparent distinctions between sites, where some earthworks index the moon and others the sun, are real and were intentional.
Given this scenario, I suspect that while the Liberty square sightline “D-F lunar” is de facto present at the earthwork, the “alignment” was not intentional. I suspect that it is a random event arising from the various combinations of gateway widths and concomitant intra-gateway azimuths.
I will now discuss the setting sightlines that are indicated by the data at the Liberty square. The group of events marked is the same as those for the rise phenomena. There is a group of three equinox lines (one of which is in error per azimuth and declination), both north and south cross-quarter sightlines are indicated, and there are a few lunar lines that constitute an incomplete set of the extrema azimuths.
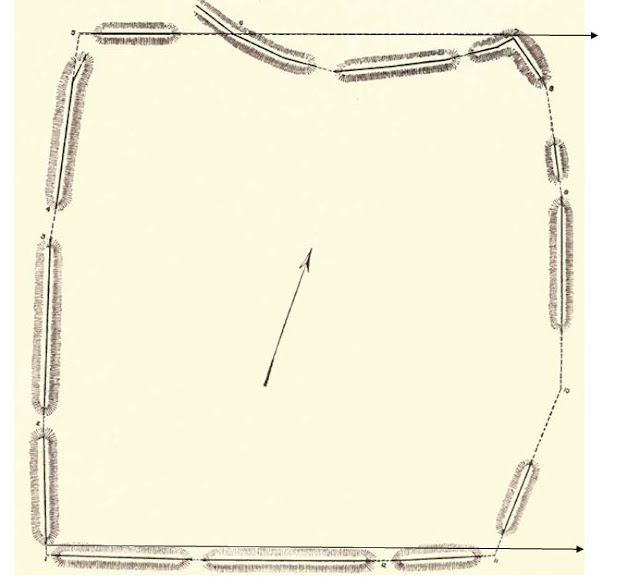
The first group is the equinox set lines. There are again three of these, using the same gateways as those of the equinox rise events (Figure 23). This is to be expected, as the corners of the square nearly index the cardinal directions and the gateways are hence almost symmetrical about the north-south axis. According to Middleton and Fowke, the azimuth from corner A to corner C is 3° 40’ (Thomas 1894:482).
Of the three, sightline F-E indexes δ = +1.0°, and is hence in error by two sun or moon widths along the horizon. The other two, sightlines G-H and B-D, index δ = -0°.1 and 0° respectively, with q = 0°. All three foresights occur on a mountain ridge about four miles distant (Figures 24 and 25). The Scioto Trails State Forest hosts some of these foresights (Figure 26).
There are three cross-quarter set sightlines indicated by the data, two north and one south. These are the sightlines B-H, F-D, and G-D, indexing declinations of +15°.8,  +15°.5, and  -15°.6 respectively with q = 0°. These sightlines are each modeled in ArcMap to utilize the embankment terminuses at both the backsight and foresight gateways (Figure 27). In analyzing an earthwork, we can situate a given sightline anywhere within each backsight and foresight that we choose, effectively selecting azimuths that “work”, but then we lose the insight gained through use of precision data. As such, throughout this analysis I have tried to reduce errors in all ways possible, thus reducing the cumulative error. One way of doing this is to standardize the placement of backsight and foresight loci at the gateway edges.
As discussed earlier, unlike solstice, there is no unique azimuth by which we can define an exact cross-quarter date. Rather we define a range and seek to determine which value was used by the Hopewell. Any repeated use of specific declination values as found at the various Hopewell earthworks may indicate both intentionality and specificity regarding which date was used. Without precision data, however, we cannot do this.
The two north cross-quarter sightlines terminate on two ridges about 3 and 3 ½ miles from the earthwork to the northwest (Figure 28 and 29), while toward the southwest, the lone south cross-quarter line sights to the top of a very salient peak. This latter sightline G-D has the highest horizon altitude value of any at Liberty, where h0 = +1.°9, and it is very precisely defined by the topographic peak feature (Figure 28 and 30).
Lastly, I discuss the lunar set sightlines. Again, as was the case with the rising events marked, there is a paucity of lines. Only two of the possible four lunar setting events are indexed, so that when combined with the rise phenomena, there are only three out of the eight lunar extrema indicated by sightlines at the Liberty square.
There are four lunar set lines resultant from the data: F-D, B-H, C-D, and G-E (Figure 32). The first two sight to the north lunar minimum set point. Romain had suggested these events at these gateways, but his published plat indicates sightlines that are in error, where δ = +16°.9 for sightline B-H, and δ = +17°.2 for sightline F-D, instead of the correct value of +18°.6 for the north lunar minimum. [Note that in Romain (1991: Figure 4) H-D and I-C are his designations for the same sightlines. Romain plots his sightlines from center-to-center of each gateway.]
The second pair of sightlines, C-D and G-E, index the south lunar maximum set event. Hence there are four setting sightlines representing only two events. There is redundancy here respecting sightline events, but still lacking is the presence of “mirror” sightlines needed to complete the full set of eight lunar extrema azimuths. That is, we do find a pair of south lunar maximum set lines, but there is no corresponding north lunar maximum set, nor a south lunar maximum rise sightline.
Again this incomplete set of lunar extrema indices suggests that these sightlines are structurally and geometrically coincident, an artifact of the design of an earthwork that marks equinoxes and cross-quarters. Just as we find a complete absence of solar sightlines at the exclusively lunar Newark octagon, shouldn’t we expect to find other earthworks that index exclusively solar events?
Arguing for the intentionality of these lunar sightlines, however, are two things. First and most simply, we do find lunar sightlines at other Hopewell geometric enclosure that are defined as occurring from gateway edge to gateway edge, as here at Liberty. Secondly, some of the lunar sightlines at Liberty appear to terminate on salient foresight terrain features (Figures 33,34, and 22). The latter may simply be and likely is an artifact of the hilly horizons presented at the Liberty earthworks.


Conclusions
It has now been thirty-five years since the first papers appeared describing Hopewell calendrical sightlines in detail. These and subsequent studies were executed using paper maps and relatively simple calculators. Today, we have sophisticated software available to perform our map and data analyses. This study of the Liberty earthworks utilizes such recent innovations, and it is with these tools that I have produced a high-precision analysis of the calendrical sightlines as defined by the gateways of the square enclosure at the site.
I have used the most accurate and precise data available for each of the many variables and constants utilized in making sightline calculations. Use of ArcMap allows for the production of many of these data. I have argued that the Middleton and Fowke survey data from the 1880s are accurate to no better than +/- 0°.1. (We will be unable to provide better estimates of the accuracy of those data until geophysical surveys are made at some of the sites that Middleton and Fowke surveyed.)
Ambiguity can be introduced into the data stream by specious use of the “q” factor in the equations. I have taken the conservative approach and standardized all sightlines, so that q = 0° in all analyses. Arbitrary use of q-values other than zero cannot be defended if an impartial unbiased data stream is intended. We cannot adopt a positive or negative q-value at each earthwork because it renders a better “fit” to the data (Hively and Horn 1982:S12, 1984:S93, 2013:85-86).
Further ambiguity occurs when we fail to precisely define what constitutes a sightline at a Hopewell enclosure. I have made every effort to establish sightlines that only use the edges of gateways as backsight and foresight indices. This follows directly from my own results at Hopeton in 1982 and from Hively and Horn’s examples at High Bank and the Newark octagon. In all cases sightlines were, or could be, accurately defined by the terminuses of the embankments.
Hively and Horn asserted that the correct calendrical lines are primarily defined by the azimuths of the embankments themselves, i.e. as occurs when sighting along the top or spine of the wall (Hively and Horn 1982:S10, S16, Table II) . These azimuths as defined by the long axes of the embankments are as readily defined by using the gateways at each end of the embankment as backsights and foresights. Hively and Horn have actually suggested both definitions as the criteria for establishing sightlines (1982: Figures 7 and 8, Table II). I choose to observe the premise of Occam’s Razor, that we opt for the more simple and elegant of interpretations, which in this case is to posit one definition for “sightline”, and one definition only: that sightlines are defined from gateway edge to gateway edge, not along the spines of the embankments also. (It is worth noting in passing that if we allowed two definitions of what constitutes a sightline, that when conducting statistical analysis of any proposed sightlines we would then effectively have to cut in half any resultant values of likelihood or probability.)
Not only am I exclusively defining sightlines as occurring from gateway to gateway, I have made every effort to define these sightlines as from gateway edge to gateway edge. I am doing this so as to not introduce further error into the analytical process. There is leeway at each gateway within which a sightline can be shifted about, to adjust it to a desired azimuth. By adhering to a strict use of gateway edges to establish sightlines, this vagary is removed.
The resultant degree of accuracy and precision achieved by all of these precautions will fully allow future researchers to test and retest these proposed sightlines in situ. I have provided precise positional data for each suggested horizon foresight. These foresights will likely be tested in the future using geophysical surveying techniques. Precision point data for each foresight loci suggested herein are fully ample as guideposts to undertaking these surveys, as well as for any subsequent archaeological excavations.
Of the seventeen sightlines proposed herein, twelve are solar and five are lunar. Among the twelve solar lines, only one does not adhere to use of a gateway edge in defining the azimuth of the sightline. This single exception, line F-D, instead utilizes the point marking the western corner of the square as a backsight (Figure 15).
Only two of the five lunar sightlines use gateway edges exclusively (Figures 22 and 31). The three other lines “float” in the middle of the gateway, not indexed by any particular feature; they point to some arbitrary direction within the opening. The solar sightlines by contrast are all (excepting one) precisely defined by the gateway edges, all with q = 0°. The non-adherence of the lunar sightlines to the edges of the gateways also argues that they are spurious. Additionally, the dearth of lunar extrema events indexed at the Liberty square suggests that those that are found are coincidental, and that they are unintended artifacts of the design inherent in the earthwork.
The lunar sightlines in some cases do terminate on the discrete terrain features that define the local horizon. None of these areas are of the highest salience, however, such as specific peaks, mountain passes, gaps, or otherwise notable terrain features. At the Liberty square, the south cross-quarter set sightline terminates precisely on a mountain peak (Figures 28 and 30). At Hopeton, the winter solstice sun emerges from a deep V-notch in the horizon profile (Turner 2011:311, Figure 9). None of the lunar horizon foresight profiles at the Liberty square are so notable. Ultimately, regarding the validity of the lunar sightlines suggested by the data, the matter will only be resolved with future archaeological testing of the various horizon foresight areas, both lunar and solar.
If these lunar lines are indeed spurious, we are left with a collection of only equinox and cross-quarter sightlines at the Liberty earthworks. They represent a complete set of such lines, i.e., there are setting and rising events noted for all of them, and there are north and south events marked. This combination of solar indices argues for an agricultural calendar. The May cross-quarter is the obvious safe planting date in the Ohio region with regard to avoiding a late freeze, while the equinox marks the earliest beginning of the spring planting season. A precise knowledge of the true calendar dates during spring would augment agricultural success and production. Myself and others have noted that the incipient use of the Eastern Agricultural Complex foods increased during the early Middle Woodland Period, coeval with the creation of the great Hopewell enclosures (Case and Carr 2008:86-88, Turner 2000, Wymer 1987). It is entirely possible if not likely that we see evidence of a developing subsistence scheduling regimen across the corpus of geometrical earthworks.
Two of the sightline pairs, D-G / D-B and G-D / G-H, share common backsights. From these backsights, the selected gateway foresight loci are each defined at the extreme ends of the opposite embankments, precisely determining the lengths of the earthwork features that are involved. During the spring, the calendar date can be easily determined from the dual backsight at gateway D (Figure 35). The daily rate of change of the sun’s rising (or setting) azimuth is greatest around equinox, and hence the daily changing sunrise azimuths are most easily distinguished one from another at this time of year. An observer would be able to closely monitor the calendar dates through the crucial agricultural planting season, between equinox and the May cross-quarter (Athens 1977). It seems likely day-counting would have been utilized by the Hopewell calendrical specialists during these crucial spring periods to determine planting times across a range of locally available micro-climates and biomes (Forde 1931, Figure 6a, Titiev 1938). There was no one single planting day.
The precision with which the sightline G-A points to a nearby mountaintop is impressive. The horizon altitude of +1°.9 is the highest among the Liberty square lines, and the sightline itself adheres to gateway edges within the earthwork enclosure. The precision with which this line can be plotted with reference to these three features is remarkable. The foresights associated with the other sightlines, while notable, lack such salience. Again, and ultimately, it will require that archaeological testing be conducted at these horizon foresight loci to pinpoint the terminuses of these various sightlines.
If we accept that the Hopewell geometric earthworks were indeed constructed and used to index particular celestial rising and setting events, then we must make sense out of why the different sites index various and seemingly complementary sets of phenomena. The two octagon shaped enclosures both mark the complete corpus of lunar extrema. The Liberty square sightlines appear to be exclusively solar. Hopeton, somewhere in design between the two, has sightlines to all of these events. We can loosely suggest that the eight-sided octagon mirrors the azimuths along the horizon that are keyed to the eight lunar extrema, while the four-sided square mirrors the pattern found with the sun and its four extrema angles, the solstice rise and sets. Note that there are also four cross-quarter “extrema”, paralleling the other solar event, the solstice. “Fourness” seems to be embodied by the sun, while “eightness” is suggested by the moon. But this latter point is merely speculation.
We also find “eightness” in the number of seasons defined by use of the cross-quarter dates as calendar markers. If the cross-quarter sightlines suggested by the data at Liberty are borne out as real, than we must accept that the Hopewell observed an eight-season annual calendar. Evidence suggesting the observance of all four of the cross-quarter dates increases the likelihood that the Hopewell calendrical specialists were heavily involved in day-counting throughout the year.
It is hoped that this paper provides not only a useful analysis of the Liberty square, but also a guide to the use of GIS in performing future archaeoastronomical analyses generally. So reluctant are the administrators of the Hopewell Culture National Historical Park to interpret these sites as “calendars”, that it will probably be well after my own death that this topic receives the attention it deserves. I suspect that this reluctance stems from an aversion to the Neo-pagans and Neo-Druids who would converge on these sites at May Day and solstice if they were promoted as an “American Stonehenge”. It is an issue of ownership of the past.
The greatest travesty in Hopewell today is the ongoing leasing of the Newark octagon site to the Mound Builder’s Country Club. Owned by the Ohio Historical Society, the lease on the site was recently renewed for an additional 75 years. It is unfathomable why an historical preservation society would lease a preeminent Hopewellian earthwork, of significance attaining to that of a World Heritage site, for use as a golf course. It is Kafkaesque to say the least. But humans are a weird lot, and there are some insane situations being perpetuated today and every day here on the planet. This is one of them.
I am and have been striving to produce detailed analysis of these fascinating earthworks for over thirty years now. I feel that it is an honor to do so. These sites are among those that defined early archaeology in America. While engaged in this field of study, rather than the experience being dignified and solemn, I have witnessed individuals making false claims in print, my Hopeton data have been plagiarized, and I have experienced the blacklisting that occurs in academia and with journals. The present format of posting articles on line with no affiliation is the best suited manner of distributing these data. I believe that the present generation of site curators and archaeologists will never acknowledge that these Hopewell enclosures were calendrical observatories. I hope that my efforts eventually encourage future researchers to pick up where our generation has failed.



References Cited

Athens, J. Stephen
1977 Theory Building and the Study of Evolutionary Process in Complex
Societies. In For Theory Building in Archaeology, edited by Lewis R.
Binford, pp. 353-384. Academic Press, New York.

Aveni, Anthony F.
1981 Tropical Archaeoastronomy. Science 213(4504):161-171.
1997 Stairways to the Stars: Skywatchng in Three Ancient Cultures. John Wiley and Sons, NY.

Braun, David
1987 Co:evolution of Sedentism, Pottery Technology and Horticulture in the
Central Midwest, 200 BC to AD 600. In Emergent Horticultural Economies of the Eastern Woodlands, edited by William F. Keegan, pp. 153-181. Center for Archaeological Investigations, Occasional Paper No. 7, Southern Illinois University at Carbondale.

Case, T.D. and Carr, Christopher
2008 The Scioto Hopewell and Their Neighbors: Bioarchaeological Documentation and Cultural Understanding. Springer, New York.

Duncan, David E.
1998 Calendar: Humanity‘s Epic Struggle to Determine a True and Accurate
Year. Avon Books, New York.

Eddy, John
1977 Archaeoastronomy of North America: Cliffs, Mounds, and Medicine
Wheels. In In Search of Ancient Astronomies, edited by Edwin C. Krupp,
pp. 133-163. Garden City, New York.

Ellegard,  A.
1981 Stoneage Science in Britain. Current Anthropology 22(2):99-125.


Fletcher, Robert V. and Terry L. Cameron
1988  Serpent Mound: A New Look at the Old Snake in the Grass.
             Ohio Archaeologist 38(1):5.

Forde, C. Daryll
1931  Hopi Agriculture and Land Ownership. Journal of the Royal          
          Anthropological Institute, LXI: 357-405.

Fowke, Gerard
1889 Popular Errors in Regard to the Mound Builders. Ohio Archaeological and
Historical Quarterly Volume 3:380-387.
1902 Archaeological History of Ohio. State Archaeological and Historical Society, Columbus, Ohio.

Greber, N’omi B.
1979  A Comparative Study of Site Morphology and Burial Patterns at Edwin
         Harness and Seip Mound 1&2. In Hopewell Archaeology: the Chillicothe
Conference, edited by David S. Brose and N’omi B. Greber, pp. 27-38.     Kent State University Press, Kent, Ohio.
1983  Recent Excavations at the Edwin Harness Mound, Liberty Works, Ross Co.,
Ohio. Midcontinental Journal of Archaeology Special Paper No. 5, Kent State University Press, Kent, Ohio.

Greenman, Emerson F.
1928 Filed Notes on the Excavation of the Eagle Mound. Manuscript of file, Ohio Historical Society, Columbus, Ohio.
1929 Archaeological Field Work In North America During 1928. American Anthropologist 31(2):213-366.

Hardman, Clark and Marjorie H. Hardman
1992 Linear Solar Observatory Theory: the Development of Concepts of Time
and Calendar. North American Archaeologist 13(2):149-172.

 Hively, Ray  and Robert  Horn
1982  Geometry and Astronomy in Prehistoric Ohio. Archaeoastronomy
supplement to the Journal for the History of Astronomy 13(4):S1-S20.
1984   Hopewellian Geometry and  Astronomy at High Bank. Archaeoastronomy
  supplement to the Journal for the History of Astronomy 15(7):S85-S100.
2013 A New and Extended Case for Lunar (and Solar) Astronomy at the   Newark Earthworks. Mid-Continental Journal of Archaeology 38(1):83-182.

Hudson, Travis
1984  California’s First Astronomers. In Archaeoastronomy and the Roots of
Science, edited by Edwin C. Krupp, pp. 11-81. Westview Press, Boulder.
1988  The Nature of California Indian Astronomy. In Visions of the Sky:
Archaeological and Ethnological Studies of California Indian Astronomy, edited by Robert A. Schiffman, pp. 5-30. Coyote Press, Salinas, CA.

Hudson, Travis, Georgia Lee, and Ken Hedges
1978 Solstice Observers and Observatories in Native California.
 Journal of California and Great Basin Anthropology, 1(1):39-63.

McCluskey, Stephen C.
1989  The Mid-Quarter Days and the Historical Survival of British Folk
Astronomy.  Archaeoastronomy supplement to the Journal for the History of Astronomy  20(13):S1-S19.
1993  Astronomies and Rituals at the Dawn of the Middle Ages. In
Astronomies and Cultures, edited by Clive N. Ruggles, pp. 163-201.      University of Colorado Press, Niwot, Colorado.

Malotki, Ekkehart
1983   Hopi Time: A Linguistic Analysis of Temporal Concepts in the Hopi Language. Mouton Publishers, Berlin.

Marshack, Alexander
1985  A Lunar-Solar Calendar Stick from North America.
  American Antiquity 50(1):27-51.
1989  North American Indian Calendar Sticks: the Evidence for a Widely
         Distributed Tradition. In World Archaeoastronomy, edited by Anthony F.
         Aveni, pp. 308-324. Cambridge University Press, Cambridge.

Marshall, James A.
1987 An Atlas of American Indian Geometry. Ohio Archaeologist 37(2):36-49.

Mills, William C.
1907 Explorations of the Edwin Harness Mound. Ohio Archaeological and Historical Quarterly, Volume 16, 113-193.

Reyman, Johnathan E.
1975   The Nature and Nurture of Archaeoastronomical Studies. In
          Archaeoastronomy in Pre-Columbian America, edited by Anthony F. Aveni, pp. 205-215.                       University of Texas Press, Austin.
1980   The Predictive Dimension of Priestly Power. In New Frontiers in
  the Archaeology and Ethnohistory of the Greater Southwest, Transactions
         of the Illinois State Academy of Science, 72(4):40-59. Edited by
  Carroll L. Riley and Basil Hedrick. Illinois State Museum, Springfield.
1987     Priests, Power, and Politics: Some Implications of Socio-ceremonial Control: In Astronomy               and Ceremony in the Prehistoric Southwest, edited by John B. Carlson. Maxwell Museum of                 Anthropology, Albuquerque.

Robertson, Thomas H.
1983 The Reliability of Historical Maps of Earthworks in the Ohio Valley.
Archaeoastronomy 6(1-4):75-79. Center for Archaeoastronomy, College Park, Maryland.

Romain, William F.
1991 Possible Astronomical Alignments at Hopewell Sites in Ohio.
Ohio Archaeologist 41(3):4-16.
1995 Further Notes on Hopewellian Astronomy and Geometry. Ohio Archaeologist  45(1):48-52.

Ruggles, Clive
1999 Whose Equinox? Archaeoastronomy supplement to the Journal for the History of Astronomy, no. 22,  pp. S45-S50.

Smith, Bruce D.
1992   Prehistoric Plant Husbandry in Eastern North America. In The Origins of
Agriculture: An International Perspective, edited by C. Wesley Cowan and Patty Jo Watson, pp. 101-119. Smithsonian Institution Press, Washington DC.

Stephen, Alexander M.
1936 Hopi Journal. Columbia University Press, NY.


Squier, Ephraim and Edwin Davis
1848 Ancient Monuments of the Mississippi Valley. Smithsonian Contributions
to Knowledge, Volume 1,  Smithsonian Institution Press, Washington DC.

Stocker, Terry
1981  A Note on Eastern U.S. Site Orientation. Archaeoastronomy 4(3):24-29.
          Center for Archaeoastronomy, College Park, Maryland.

Thomas, Cyrus
1889 The Circular, Square, and Octagonal Earthworks of Ohio. Bureau of
Ethnology Bulletin, No. 10, Washington DC.
1894  Report on the Mound Explorations of the Bureau of Ethnology. Twelfth
  Annual Report of the Bureau of American Ethnology, Washington DC.

Thomas, Michael E. and Richard I. Joseph
Astronomical Refraction. Johns Hopkins APL Technical Digest 17(3):279-284

Titiev, Mischa
1938 Dates of Planting at the Hopi Indian Pueblo of Oraibi.
Museum Notes, Museum of Northern Arizona 11(5):39-42.

Turner, Christopher S.
        1982   Hopewell Archaeoastronomy. Archaeoastronomy 5(3):9.
                    Center for Archaeoastronomy, College Park, Maryland.
         1983  An Astronomical Interpretation of the Hopeton Earthworks.
                     Manuscript on file at the Hopewell Culture National Historical Park,
                    Chillicothe, Ohio; and at the Ohio Historical Center, Columbus.
                     This and other my papers are available online at <Hopewell Archaeology and                                        Archaeoastronomy>, easily found using Google.
        2000   Toward a Model of Hopewell Subsistence Scheduling: the Geometrical Earthworks of                          Ohio as Calendrical Devices. This and other papers are available online at <Hopewell                          Archaeology and Archaeoastronomy>.
         2004 Statistical Analysis of Hively and Horn’s Claims at the Newark Octagon. Poster presented                     at the Midwest Archaeological Conference, St. Louis, MO. This and other papers are                            available online at <Hopewell Archaeology and Archaeoastronomy>.
2011 Ohio Hopewell Archaeoastronomy: a Meeting of Earth, Mind, and Sky.                                                 Time and Mind 4(3):301-324. A free PDF of this article can be found online.

Wymer, Dee Anne
1987  The Paleoethnobotanical Record of Central Ohio- 100BC to AD 800: Subsistence Continuity and Cultural Change. Unpublished PhD Dissertation, Department of Anthropology, Ohio State University, Columbus.
Zeilik, Michael
 1985  The Ethnoastronomy of the Historic Pueblos, I. Calendrical Sun
Watching. Archaeoastronomy supplement to the Journal for the History of Astronomy, 16(8):1-24.















Tables
Table 1
Gateways        Azimuth      Declination       Error Event       /       Declination
D to C 51°.2 30°.3 1°.5 North Max Rise          +28.8
C to D 231.0 -27.8 1.0 South Max Set            -28.8
G to E 227.8 -30.0 1.2 South Max Set           -28.8
B to A 227.1 -30.5 1.7 South Max Set           -28.8
B to H 290.5 +16.9 1.7 North Min Set          +18.6
F to D 290.9 +17.2 1.4 North Min Set           +18.6
________________________________________________________________________

These six sightlines are from Romain (1991: Figure 4). The gateway designations are shown in Figures 2 and 9. The azimuths are obtained using the COGO editor in ArcMap. I georeferenced a JPG of Romain’s plat (1991: Figure 4) and overlaid line shapefiles on his “alignments”, determining their bearings with the COGO Report direction and distance tool. The declination figure results from analyses with the archaeoastronomical calculations outlined in the article. The postulated celestial event and associated “correct” declination are in the last column.







Key to Tables 2 and 3

Backsight: Location where observer stands. Nomenclature based on the survey
                         stations as defined by Middleton/Fowke 1880s survey (Thomas 1894).
Foresight: Gateway toward which observers sights.

A: True azimuth of sightline

h0: Horizon height as seen along sightline from specified backsight.

Event: Indicates event indexed by sightline, e.g:

EQ =   equinox
CQ = cross-quarter date, north(n) or south (s)
LN = lunar minimum
LX = lunar maximum

d: Declination

q: All sightlines are calculated with q = 0







Table 2:

Liberty Square Calendrical Sightlines  (Rising Phenomena)


Backsight/Foresight A h Event declination  

D to B 90.3                0.84 EQ                     0.0
E to F 91.1                  0.75 EQ           -0.7    
H to G 90.6    0.82 EQ     0.0    
D to G 70.6                 1.00 CQn +15.3  
D to F 111.0                1.29 CQs -15.3    
H to B 111.1                  1.20 CQs -15.6  
D1 to F 115.9                   1.15 LNs -18.6      
 







Table 2:
Liberty Square Calendrical Sightlines (Setting Phenomena)
Backsight/Foresight A                        h Event declination

B to D 269.4 1.06 EQ                           0.0    
F to E 270.8 1.06 EQ +1.0    
G to H 269.5 1.16 EQ +0.1    
B to H 290.2 0.84 CQn +15.8    
F to D 289.8 0.87 CQn +15.5    
G to D 248.3 1.91 CQs -15.6    
F to D 293.1 0.88 LNn +18.6    
B to H 292.9 1.07 LNn +18.6    
C to D 229.5 1.25 LXs -28.8    
G to E 229.6 1.22 LXs -28.8      








Figures

 Figure 1. The Liberty Earthworks illustrated from Squier and Davis (1848). East is erroneously up in the figure, leading to criticism of the accuracy of their maps. They are imprecise with regard to archaeoastronomical analyses, (the embankment bearings and dimensions are inaccurate), but are otherwise of excellent quality. Appended below is an excerpt from Squier and Davis, page 56. Note how they comment on the levelness of the ground upon which the square is located. The interior of the square appears flat in comparison to the surrounding terrain when examined in ArcMap hillshade imagery (Figure 6). Squier and Davis go on to note the many pits found within the perimeter of the square saying that their presence is “a very unusual circumstance.” It is likely that the interior of this enclosure as well as those at other sites were terra-formed by the Hopewell to approach some degree of levelness before earthwork construction.

Figure 1b. Excerpt from Ancient Monuments pertaining to the Liberty site (Squier and Davis 1848:56). The large mound referred to is the Harness Mound, one of the larger Hopewell mortuary tumuli.

Figure 2. The plat of the Liberty earthworks square enclosure (Thomas 1894:482). According to the accompanying survey data, the distance A-B, B-C, C-D, and D-A  are 1008, 1006, 1110, and 1002 feet respectively. Squier and Davis (1849:56) asserted that all four sides of the square were 1080 feet. They also noted that the height of the embankments was no more than four feet, which agrees with Thomas (1894:483). The interior mounds are 125-135 feet from each nearest respective gateway when measured in ArcMap, different from the forty-foot figure quoted in Ancient Monuments. Squier and Davis list the gateway widths as all being 40 feet. As measured in ArcMap, two gateways have that width from embankment brow-to-brow, but the rest are wider up to 112 and 150 feet. The text in Thomas (1894) does not list the gateways widths among the survey data. I have seen figures for gateway widths at the National Anthropological Archives in the Middleton/Fowke field notes (Manuscript #2400, accessed 1982). However, I do not presently have copies of those data. It is evident that these gateway widths were recorded during the 1880s survey and that those figures were used in the drawing of the plats. In my analyses I designate five of the gateways A through E following the plat, and label the remaining three gateways F, G, and H as shown above (see also Figure 9).

Figure 3. Diagram of the Newark Octagon earthworks from Hively and Horn (1982:14). They noted how embankment A-H is shorter than the others, effectively widening gateway H and rendering the terminus of the wall, or gateway edge, an effective backsight for the proposed sightline. Note how they comment on the various gateway widths.

Figure 4. The Middleton/Fowke plat with all sightlines plotted. I will discuss these later with specificity. Note here that nearly every gateway edge serve as either a sightline backsight or foresight. The blue lines indicate setting events, red for rising.

Figure 5. Poor quality reproduction of margin notes from National Anthropological Archives (MS #2400), field notes from the Middleton/Fowke survey. Drawing represents the northwest corner of the Hopeton “square” enclosure. Normally flat gateway interior has a smaller sub-embankment extending from the adjacent wall, effectively narrowing the gateway to a precise backsight. This is the backsight locus for the winter solstice sunrise (and south lunar maximum rise) as seen from Hopeton (Turner 2000, 2011). Written in the field notes describing this drawing: “Northwest corner of square has opening somewhat higher than natural surface…Low middle is highest at north side of opening even with the middle of the bank & slopes down to a narrow point at the inside of bank on opposite wall.” (See Figure 7 for larger map of Hopeton enclosure.)

Figure 6. Hillshade view from ArcMap showing traces of the Liberty earthworks. Upper illustration has pink line showing location of square. Small circle as shown in Figure 1 is clearly visible to the lower left of the square. (Note that in Figure 1 east is at the top, not north as in this image.) Other visible linear features are of railroads, highways, and fence lines. A major rail line bisects the square from upper left to lower right.

Figure 6b. From Stephen (1936), map 4. Looking southwest to sunset over the San Francisco Peaks as seen from Walpi pueblo, showing the specific foresight features of the horizon profile. Note the use of peaks and notches for indexing particular dates. The low gap (left center) marked “Decr 10th” (December tenth) marks the beginning of the ceremonial period associated with the winter solstice. The daily shift of the sun’s position along the horizon drops to zero as the sun turns around at solstice, becoming unobservable for four days. Therefore the advance ten-day warning provides a method for determining the precise date for the true solstice. After witnessing the “Decr 10”-notch sunset, day-counting would then be utilized to mark the ten-day interval, so that any attendant rituals or dances associated with the winter solstice could be executed at their proper times.

Figure 7. Middleton/Fowke plat of the Hopeton earthworks. The north and south sides of the Hopeton polygon index the May cross-quarter date sunrise (Turner 2000, 2011). The upper left corner of the enclosure is discussed in Figure 5.

Figure 8a. The Fairground Circle, 0.3 meter elevation contours. Note the central mound, the so-called “Eagle Mound”. The enclosure embankment is darker green, the interior ditch whitish. The single gateway is at upper right, with causewayed entrance. Note borrow pit feature at lower right.

Figure 8b. Detail of Fairground Circle gateway and central Eagle Mound. Red dots are sub-mound postmolds located by Greenman in 1928. White cross is centroid of enclosure embankment as calculated in ArcMap. Small arrows at entrance walls indicate lunar sightlines suggested by Hively and Horn (1982:S15-S16, Table II). These walls are far too short to function as calendrical sightlines, and the authors retracted the assertion for that reason in their 2013 article (page 96).

Figure 8c. Detail of axial sightline at the Fairground Circle. This sightline indexes the sunrise at the May cross-quarter date. It does not index summer solstice rise as attested by Stocker (1981). It misses the north lunar minimum risepoint by more than three degrees. Hively and Horn (2013:96) assert that the Fairground Circle axial sightline is difficult to accurately establish visually due to the architecture of the earthworks. This is incorrect. Note the multiplicity of features at the centrally located Eagle Mound that serve as backsight loci guides. Note how easy it is to define the midpoint of the entrance causeway and hence the associated azimuthal bearing as seen from the Eagle Mound locus. The causeway itself, the ditch, and the embankments all serve as indices in establishing gateway axiality at the earthwork. Note also that it is simply very easy to sight the gateway from the Eagle Mound when making on-site observations.

Figure 8d. View at sunrise on May 4, 1999. Visible are the rising sun, the entrance causeway, the flanking interior ditches, the termini of the embankments, and the northeastern segment of the Eagle Mound in the foreground. The Hopewell certainly had felled all of the trees that would have interfered in the construction of the earthworks, and those that blocked useful sightlines, so this sightline would have been extremely easy to define, even more so than it is today. This photograph was taken by Michael Van Dorn of Newark, Ohio.

Figure 8e. View from outside of gateway looking into entrance of the Fairground Circle. The Eagle Mound is visible in the distance. In the foreground are visible the causewayed entrance, the interior ditches or moats, and an embankment slope on left. I took this photograph in 1982.

Figure 8f. View from top of embankment looking across causewayed entrance showing the opposite curving embankment, ditch, and edge of the terra-formed interior. I took this photograph in 1982.

Figure 8g. Created in ArcMap, this image shows the axial sightline at the Fairground Circle and associated horizon foresight. Line is coded green where local topography is visible from Eagle Mound backsight. The specificity with which this sightline converges on the salient bluff feature at right supports the idea that these sightlines were intentionally created and used by Hopewell calendrical specialists or elites.

 Figure 9. Thomas (1894) Liberty square plat with sightlines as per Romain (1991: Figure 4). Note gateway designations (which differ from those used in Romain’s 1991 article).

Figure 10. Sightline as plotted with Romain’s  listed azimuth value of 53.2 degrees (1991: Figure 4), with backsight located at corner of gateway D. Note that sightline does not go through foresight gateway C as Romain suggested, but instead is obstructed by the adjacent embankment. The sightline is about 35 feet from the gateway edge where obstructed. Note that backsight gateway D has no extra room to allow adjustment of the sightline to function correctly with respect to gateway C as foresight. The sightline cannot be moved west, maintaining the proper azimuth, correctly passing through foresight gateway C, and still utilize gate D as a backsight.

Figure 10b. From Forde (1931), a plot of the horizon profile as seen from the Hopi pueblo of Walpi, showing attendant subsistence events at corresponding dates. Forde wrote that “For ..the Hopi of Walpi such terms as neverktcomo and  lohalin have as precise a significance  as have for us May 3rd or June 21st with which they correspond.” Note the indexicality of the horizon terrain features. Horizon calendars lacking monumental architecture were probably ubiquitous worldwide across cultures. They existed only in the minds of their users. One need only define a precise location from which to make the observations, the so-called backsight. The foresights then are all defined by the natural features along the horizon.

Figure 11. The environs of the Liberty earthworks, dimensions about 8 by 3 ¾  miles. Blue outline in center is Liberty square. Elevation contours are 40 feet. Green dots are sightline foresight loci. Broad light blue area is the floodplain of the Scioto River, which runs along the base of the bluff line at left.

Figure 12. The equinox rise sightlines suggested by the data. Note the gateway nomenclature A through H, following that of Middleton and Fowke with variations.

Figure 13. Sightline E-F is in error with regard to the equinox rise: the sightline indexes declination -0°.7. I reconstructed the elevation contours for the road-cut feature near the right center of the image using a pre-disturbance USGS topographic map. The E-F sightline passes directly over this disturbed area. The reconstructed area did not obscure the more distant ridgeline to the east as seen from the Liberty site. In any case, this sightline as already noted is in error by seven-tenths degrees declination. The foresight loci for the two other sightlines are unique. Both foresights are less than a mile from the square enclosure, where usually these foresights are on much more distant ridges or mountains. Elevation contours are 30 feet.

Figure 14. Detail of foresight area for sightlines H-G and D-B. Elevation contours are ten feet. UTM coordinates are shown for the foresight points, NAD 1927, zone 17. These sightlines precisely index the equinox sun at half-risen, or for q = 0. Note that each line terminates on a salient topographic feature. Highway construction has destroyed southern segment of ridge, but these foresights were spared.

Figure 15. See Figure 12 for gateway nomenclature. Note that sightline D-F uses the corner of the square for a backsight, not the edge of a gateway as with all of the other solar lines.

Figure 16. This sightline is also relatively short, and it too crosses a disturbed area, this time a railroad cut. The declination indicated by this sightline is +15°.3 for q = 0°. This corresponds to a sunrise date May 2. This differs by two days as compared to the Fairground Circle sightline.

Figure 17. Foresight locus of sightline D-G. Purple shaded areas are within viewshed of Liberty earthworks gateway D, the backsight of this sightline. Note curved railroad cut across map. The original foresight location may have been at the railroad cut and may have been destroyed. Elevations are in feet. Coordinates are given for the proposed foresight locus in UTM NAD 1927 zone 17.

Figure 18. All seven of the Liberty square rise event foresights are shown in this map as light green dots. The sightlines shown (H-B and D-F) index declinations of -15°.6 and -15°.5 respectively, with q = 0°. These correspond to sunrises in early February and early November, at two of the four cross-quarter dates. If a consistent use of the May cross-quarter date can be demonstrated across Hopewell geometric sites, a subsistence scheduling calendar can be suggested. If these other cross-quarter date sightlines are repeatedly demonstrated, a broader use of the cross-quarter calendar throughout the entire year is then implicit.

Figure 19. Note that sightline D-F terminates atop a very salient peak feature. Contours are 10 feet. UTM NAD 1927 zone 17 coordinates are provided for the foresight loci.

Figure 20. ArcScene view of the two lines-of-sight D-F (right) and H-B (left). The Middleton/Fowke plat of the Liberty square is draped onto the DEM surface, but has no height features otherwise: the embankments are flat. Even so, this view gives a good impression of the azimuth selection capabilities using the embankment features.

 Figure 21. Another view of sightline D-F. Note the prominence of the horizon features. Vertical height is not exaggerated.

Figure 22. The sightline above, “D-F lunar”, does indeed index the south lunar minimum moonrise exactly (with q = 0°, δ = -18°.6). It seems unlikely that this was intentional however, as there is a complete lack of all other lunar extrema rise lines present. Notably lacking are any lunar maxima rise sightlines. These maxima events are far more observationally salient than the lunar minima, as they possess extreme azimuths that exceed those along the horizon of the sun at the solstices. The lunar minima rise points occur within the azimuthal sweep of the sun and moon on the horizon, and are hence less distinguishable. As based on its observational salience, we should expect recognition of the lunar maxima to occur before recognition of the lunar minima (Aveni 1981:161, 1997:21-2, Ellegård 1981: 101-2, Hardman and Hardman 1992).






Figure 23. The Liberty square equinox set sightlines. Refer to Figure 12 for gateway nomenclature. These backsight loci are around 620 feet in elevation ASL. Note that sightline F-E is in error by one-degree in declination (δ = +1°.0). Observe how this sightline cannot be moved any further in azimuth to negate the error, as it lies at the extreme edges of its backsight and foresight gateways.

Figure 24. At around 1000 feet in elevation, the foresight ridge lies about 3.9 miles from gateway B.











Figure 25. Detail of foresights with viewshed in pink. These pink-coded areas are visible from gateway D. Nearly identical viewshed coverage is indicated for gateways F and G.











Figure 26. From north to south, these foresights are for sightlines G-H, F-E, and B-D. Two of these are located in Scioto Trails State Park, and are protected. The UTM coordinates are for NAD 1927, zone 17. These point data are intended to guide future researchers in locating and archaeologically testing these areas for evidence of their use as sightline foresights.








Figure 27. The cross-quarter date setting sightlines as indicated by the data for the Liberty square. Note how the southern edge of gateway D is used as a backsight for both the south and north cross-quarter lines, while the backsights are defined by the northern edge of gateway G, and the southern edge of gateway F.









Figure 28. Pink shaded areas are viewshed coverage as seen from gateway B.












Figure 29. These May and August cross-quarter set sightlines terminate at elevated peak and ridge features. The Scioto River lies at the foot of the bluff to the east.











Figure 30 and detail. Foresight locus for the south cross-quarter date sightline G-D. Shaded pink areas are viewshed coverage as seen from gateway B. Use of this peak feature as a foresight yields the highest value of horizon altitude for any sightline at the Liberty square, with h0 = 1°.9.






Figure 31. Represented are two each of the lunar minimum north and lunar maximum south sightlines. These are sightlines B-H and F-D (lunar minimum north) and C-D and G-E (lunar maximum south). Note that of these four sightlines indicated, three of them do not exclusively use gateway edges to define the correct azimuth (and hence declination). Of the twelve solar lines suggested by the data, only one cannot be accurately and precisely defined by using gateway edges as backsights and foresights.








Figure 32. All ten of the foresight loci for the setting phenomena discussed herein are indicated on this map by light green dots. The two south lunar maximum foresights occupy a low level ridge (bottom right center), while the two north lunar minimum loci share a ridge with one of the north cross-quarter foresights.











Figure 33. The two sightline foresights have coordinates indicated in UTM NAD 1927 zone 17 format.











Figure 34. These are the foresights for the two south lunar maximum sightlines indicated by the Liberty square data. Contours are ten feet, coordinates UTM NAD 1927 zone 17.










Figure 35. Combination backsight for cross-quarter sightline D-G and equinox sightline D-B.